ユークリッド原論をどう読むか（６）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー６（円と接する円、直線）　　
(接する２円の接点と中心は１直線上)
(中心は接線の接点での垂線上)
(円周上から半径に垂直な直線は接線)
(円外の点から引いた接線は２本)
(接する２円の接点での接線は一致)
(接する２円の接点は１つ)
もし
　二つの円が
　互いに接するならば、
それらは
　同じ中心をもたないであろう。

• 円は定義１ー１５による。
• 接するは定義３−３による。
• 中心は定義１ー１６による。

２円ＡＢＣ、ＣＤＥが
　点Ｃにおいて
　互いに接するとせよ。
それらは
　同じ中心をもたないであろう
　と主張する。
　


［２円が接するとき、
　 互いに他の外部にある場合
　 一方が他方の内部にある場合と、
　がある。
互いに他の外部にある場合、
　中心が
　それぞれの円の内部にあることにより、
　他の円の外部にあるから、
　同じ中心とはなりえない。
一方が他方の内部にある場合、
　すなわち、
　円ＡＢＣがＣＤＥを内部に含む場合を
　以下に証明する。］

• 定義３ー３により、
  　２円は交わらないから、
  　一方が他方の内部にあるか、
  　外部にあるかどちらかである。

もし可能ならば

• 背理法の仮定を述べようとしている。
• 「もし可能ならば」は、
  コメント２(命題１−７）参照のこと。

同じ中心をＦとし、

• 「Ｆをとり」ではなく、
  　「Ｆとし」であることに注目すること。

ＦＣが結ばれ

• 公準１ー１による。

任意に
　ＦＥＢがひかれたとせよ。 【・・・(a)】

• 円ＡＢＣはＣＤＥを内部に含むので、
  　ＣＤＥの外部となる円周上の部分があり、
  　公準１ー１の補足により点Ｂをとる。
  このＢと中心とを
  　公準１ー１により結ぶ。
  ＣＤＥの内部にある中心Ｆと
  　外部のＢを結ぶ線分は
  　命題３−２の補足により
  　ＣＤＥの円周と交点をもつ。
  それをＥとする。 【・・・(b)】
  　Ｂ、Ｅを溯って使用している。

そうすれば
点Ｆは
　円ＡＢＣの中心であるから、
ＦＣは
　ＦＢに等しい。 【・・・(1)】

• (a) ,定義１ー１５による。

また
点Ｆは
　円ＣＤＥの中心であるから、
ＦＣは
　ＦＥに等しい。

• (a) ,定義１ー１５による。

しかも
　ＦＣがＦＢに等しいことも
　先に証明された。

• (1) による。

それゆえ
　ＦＥもＦＢに、
　すなわち小さいものが大きいものに等しい。

• (b) ,公理１ー１、公理１ー８による。

これは不可能である。
ゆえに
　点Ｆは
　円ＡＢＣ、ＣＤＥの中心ではない。
　
よって
　［ ２つの場合の結果から、 ］
　もし
　二つの円が互いに接するならば、
　それらは同じ中心をもたないであろう。
　
これが証明すべきことであった。
　
　

• ２つの異なる円が
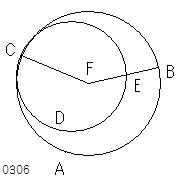
  　点Ｃにおいて接するならば、
  　接点と２つの中心は１直線上にある。
  逆に、
  　２つの異なる円の共有点と
  　　２つの中心が１直線上にあるならば、
  ２つの異なる円は
  　点Ｃにおいて接する。
  　（以下、命題３ー６の補足(接する２円の接点と中心は１直線上)という。）
  定義３ー３により、
  　２円は交わらないから、
  　 　一方が他方の内部にある場合と、
  　 　互いに外部にある場合
  　がある。
  ］
  [ 一方が他方の内部にある場合、]
  　点Ｃで接するとすると
  　以下のとおりである。
  　すなわち、
  　円ＡＢＣがＣＤＥを内部に含むとする。
  命題３ー１により、
  　円ＡＢＣ、ＣＤＥの中心を
  　それぞれＦ、Ｇとする。 【・・・(0101a)】
  
  
  
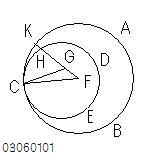
  背理法の仮定として、
  　Ｃ、Ｆ、Ｇが１直線上にないとすれば、
  　ＦとＧ、ＧとＣ、ＣとＦをそれぞれむすぶと、
  　重ならないので、
  　三角形ＣＦＧができる。
  よって、
  　命題１ー２０により
  　ＦＣはＦＧとＧＣの和より小さい。 【・・・(010101)】
  一方、 公準１ー２により
  　線分ＦＧをＧの方向に延長すると、
  　命題３−２の補足により
  　円ＣＤＥと交わり、
  　その交点をＨとする。
  また、
  　円ＡＢＣと交わり、
  　その交点をＫとする。 ＣＤＥは
  　ＡＢＣの内部にあるから
  　線分ＦＫ上に線分ＧＨがある。 よって、
  線分ＦＫは
  　ＦＧとＧＨとの和ＦＨに等しいか、より大きい。
  (0101a) ,定義１ー１５により、
  　ＧＨはＧＣに等しいので、
  　ＦＫは
  　ＦＧとＧＣとの和（ＦＨ）に等しいか、より大きい。
  ところが、
  　(0101a) ,定義１ー１５により、
  　ＦＫはＦＣに等しく、
  　(010101) により
  　ＦＣは
  　ＧＣとＦＧの和より小さい。
  これは不可能である。
  したがって
  　背理法により、
  　Ｆ、Ｇ、Ｃは
  　１直線上にあることが証明された。
  
  逆に、
  　円ＡＢＣ、ＣＤＥの共有点Ｃと
  　　それぞれの中心Ｆ、Ｇが
  　１直線上にあるとする。【・・・(0102a)】
  
  
  
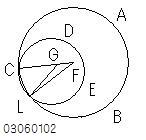
  背理法の仮定として、
  　ＡＢＣの円周とＣＤＥの円周が
  　Ｃ以外の共有点Ｌをもつとする。
  三角形ＦＬＧにおいて、
  ＦＬは
  　命題１ー２０により
  　ＦＧとＧＬの和より小さい。 【・・・(010201)】
  (0102a) ,定義１ー１５により、
  　ＧＣはＧＬに
  　等しいので、
  　公理１ー８の補足２により
  ＦＬは
  　ＦＧとＧＣの和より小さい。
  一方、
  　Ｃ、Ｆ、Ｇは
  　１直線上にあるから、
  　公理１−７により
  ＦＣは
  　ＦＧとＧＣの和に等しく、
  　(0102a) ,定義１ー１５により、
  　ＦＬはＦＣに等しいので、
  　ＦＬはＦＧとＧＣの和に等しい。
  ところが、
  　(010201) により、
  　ＦＬはＦＧとＧＬの和より小さい。
  これは不可能である。
  背理法により
  　円ＡＢＣとＣＤＥの共有点は
  　Ｃ以外にないので、
  　２円は
  　接する。
  
  [ 互いに外部にある場合、]
  　点Ｃで接するとすると、
  　以下のとおりである。
  命題３ー１により、
  　円ＡＢＣ、ＣＤＥの中心を
  　それぞれＦ、Ｇとする。 【・・・(0103a)】
  
  
  
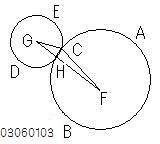
  背理法の仮定として、
  　Ｃ、Ｆ、Ｇが１直線上にないとすれば、
  　ＦとＧ、ＧとＣ、ＣとＦをそれぞれむすぶと、
  　重ならないので、
  　三角形ＣＦＧができる。
  よって、
  　 　命題１ー２０により
  　ＦＧはＦＣとＣＧの和より小さい。 【・・・(010301)】
  一方、
  　円ＡＢＣの外部にＧがあるから、
  　線分ＦＧと円ＡＢＣは交わり、
  　その交点をＨとすると、
  ＣＤＥの円周は
  　ＡＢＣの内部を通らないから
  ＨはＣＤＥの内部ではないので、
  (0103a) ,定義１ー１５により、
  線分ＦＧは
  　ＧＣとＦＣの和に等しいか
  　それより大きい。
  ところが、
  　(010301) により、
  　ＦＧはＦＣとＣＧとの和より小さい。
  これは不可能である。
  　背理法により、
  Ｃ、Ｆ、Ｇは１直線上にある。
  
  逆に、
  　円ＡＢＣ、ＣＤＥの共有点Ｃと
  　　それぞれの中心Ｆ、Ｇが
  　１直線上にあるとする。
  ＡＢＣ、ＣＤＥが
  　Ｃ以外に共有点Ｍをもったとする。 【・・・(0104a)】
  
  
  
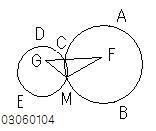
  三角形ＭＦＧにおいて、
  　命題１ー２０により、
  ＦＧは
  　ＭＦとＭＧの和より小さい。
  (0104a) ,定義１ー１５により、
  ＭＧはＧＣに、
  　ＭＦはＣＦに等しいので、
  　公理１ー８の補足２により
  ＦＧは
  　ＧＣとＦＣとの和より小さい。 【・・・(010401)】
  一方、
  　Ｃ、Ｆ、Ｇは１直線上にあるので、
  　公理１ー７により、
  　ＦＧは
  　ＦＣとＣＧとの和に等しい。
  ところが、
  　(010401) により、
  　ＦＧはＦＣとＣＧとの和より小さい。
  これは不可能である。
  背理法により、
  　円ＡＢＣとＣＤＥは
  　Ｃ以外に共有点がないから、
  　接する。
  ２つの場合の結果により
  　成立する。
  　
  　
• 円ＡＢＣに直線ＤＣＥが接するならば、
  　接点Ｃにおける接線の垂線ＣＦ上に、
  　円の中心Ｇがある。
  　（以下、命題３ー６の補足２(中心は接線の接点での垂線上)という。）
  
  
  
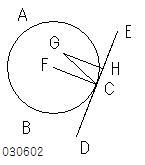
  背理法の仮定として、
  　円ＡＢＣの中心Ｇが
  　垂線ＣＦ上にないとすれば、
  　命題１ー１２により
  　接線ＤＣＥに中心Ｇから垂線をおろすと、
  　接点と異なる点Ｈにおりる。 【・・・(0201)】
  三角形ＧＣＨにおいて、
  　角ＧＨＣは直角であり、
  　ＧＣＨはＧＨＣより小さい。
  　命題１ー１９により
  　線分ＧＨは
  　接点Ｃと中心Ｇとを結ぶ線分ＧＣより小さい。
  定義１ー１５により、
  　この点Ｈは円ＡＢＣの内部にある。
  ところが、
  (0201) , 定義３ー２により
  　Ｈは円ＡＢＣの内部にはない。
  これは不可能である。
  背理法により
  　接点における接線の垂線上に
  　中心がある。
  　
  　
• 円周上の点Ｃをとおり
  　半径ＤＣに垂直な直線ＥＣＦは
  　円ＡＢＣに接する。
  　（以下、命題３ー６の補足３(円周上から半径に垂直な直線は接線)という。）
  
  
  
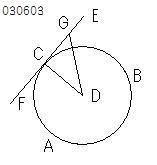
  円周上の点Ｃをとおり
  　半径ＤＣに垂直な直線ＥＣＦ上に、
  　半径との交点Ｃ以外に、
  　公準１ー１の補足により、
  　任意に点Ｇをとる。
  公準１ー１により
  　ＧとＤとを結ぶ。
  三角形ＣＤＧにおいて、
  　角ＤＣＧは直角だから、
  　ＤＧＣより大きい。
  命題１ー１９により
  　ＤＧは半径ＤＣより大きく
  　定義１ー１５により、
  　Ｇは円の外部にある。
  したがって、 直線ＥＣＦは
  　Ｃで円と会し、
  　その他の点は円の外部となり、
  　　円を切らないから、
  　定義３ー２により
  　円と接する。
  　
  　
• 円ＡＢＣの外の点Ｄから
  　円に引いた接線は
  　２本であり、
  　円外の点と接点とを結ぶ２線分は等しい。
  　（以下、これを命題３ー６の補足４(円外の点から引いた接線は２本)という。）
  
  
  
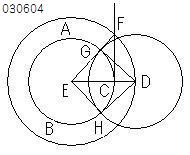
  命題３−１により
  　円の中心Ｅをとる。 【・・・(04a)】
  公準１−１により、
  　ＤとＥとをむすぶ。
  Ｅは円の内部、
  　Ｄは円の外部にあるから、
  　命題３−２の補足により
  　線分ＤＥは円周と交わる。
  その交点をＣとする。
  命題１ー１１により、
  　線分ＥＤに垂直に、
  　Ｃから直線ＣＦをひく。 【・・・(04b)】
  ＣＦは
  　命題３-６の補足３により、
  　円ＡＢＣの接線となる。
  また、
  　公準１−３により、
  　中心Ｅ、半径ＥＤの円をかく。 【・・・(04c)】
  点Ｃは
  　この円の内部にあり、
  　命題３−２の補足により、
  　ＣＦはこの円と交わる。
  その交点を改めてＦとする。
  公準１−１により
  　ＦとＥとをむすぶ。
  ＣＦは接線であるから、
  　定義３-２により、
  　Ｆは円ＡＢＣの外部の点である。
  一方
  　Ｅは内部の点であるから、
  　命題３−２の補足により
  　線分ＥＦは円ＡＢＣと交わる。
  その交点をＧとする。
  公準１−１により、
  　ＧとＤとをむすぶ。
  三角形ＥＣＦとＥＧＤとにおいて、
  　２辺ＥＣ、ＥＦと
  　ＥＧ、ＥＤは
  　(04a) (04c) により、
  　それぞれ等しく、
  　角ＣＥＦとＧＥＤは
  　共通だから、
  　命題１−４により、
  　角ＥＣＦとＥＧＤは等しい。
  角ＥＣＦは
  　(04b) により、
  　直角に等しいから、
  　角ＥＧＤも直角に等しい。
  直線ＧＤは
  　半径ＥＧに直角となるので、
  　命題３−６の補足３により、
  　円ＡＢＣに接する。
  そこで、
  　公準１−３により
  　中心Ｄ、半径ＧＤの円をかく。
  命題１−７により
  　円ＡＢＣと、
  　直線ＥＤについて
  　両側にひとつずつ２点で交わる。 【・・・(0401)】
  Ｇ以外の点をＨとする。
  公準１−１により、
  　ＥとＨ、ＤとＨを結ぶ。
  三角形ＥＧＤとＥＨＤにおいて、
  　３辺がそれぞれ等しいから、
  　(0401) ,命題１−８により、
  　角ＥＧＤとＥＨＤは等しく、
  　ＧＤ、ＨＤも等しい。 【・・・(0402)】
  よって、
  　ＥＨＤは直角に等しく、
  　直線ＨＤは
  　半径ＥＨに垂直だから、
  　命題３−６の補足３により、
  　円ＡＢＣに接する。
  また、
  　ＧＤ、ＨＤが等しいことも
  　(0402) に示された。
  さらに、
  　命題１ー４７により、
  　ＧＤに不等な線分では
  　ＥＧ、ＥＤとによって
  　直角三角形とならないので、
  　Ｄを通る接線とならない。
  よって、
  円の外部にある点を通る接線は
  　ただ２本あり、
  外部の点と２接点とを
  　それぞれ結ぶ２線分は
  　等しい。
  　
  　
• 二つの異なる円が
  　ある点で接するならば、
  　その点での接線が一致する。
  逆に
  　異なる２円の
  　　ある点での接線が一致すれば
  　その点で
  二つの異なる円は
  　接する。
  　（以下、これを命題６の補足５(接する２円の接点での接線は一致)という。）
  ２つの円をＡＢＣ、ＣＤＥとし、
  　接点をＣとする。
  
  
  
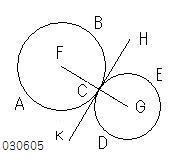
  命題３−６の補足により、
  　それぞれの中心Ｆ、ＧとＣが１直線上にある。
  命題３−６の補足３により、
  　円ＡＢＣのＣにおける
  　　接線ＣＨは
  　半径ＦＣに垂直である。
  また、
  　ＣＤＥの接線ＣＫは
  　半径ＧＣに垂直である。
  ＧＣは
  　ＦＣ上にあるので、
  ＣＨ、ＣＫとも
  　ＦＣに垂直である。
  直線ＦＣについて、
  　ＨとＫが
  　 同じ側にある場合と、
  　 異なる側にある場合、
  　がある。
  ＨとＫが
  同じ側にある場合
  　角ＦＣＨとＦＣＫは
  　直角で等しいので、
  　公理１ー７の補足により、
  　重なり合い、
  直線ＣＨとＣＫは
  　重なり合う。
  ＨとＫが
  異なる側にある場合
  　角ＦＣＨとＦＣＫは
  　直角で等しいので、
  　命題１ー１４により、
  ＣＨとＣＫは
  　互いに１直線をなす。
  したがって、
  ２つの場合の結果により
  　接線ＣＨとＣＫは一致する。
  逆に
  　異なる２円ＡＢＣ、ＣＤＥの
  　　共有点Ｃでの接線ＣＦが一致するとする。
  命題３ー６の補足２により、
  　それぞれの中心Ｇ、Ｈは
  ＣＦに垂直な直線ＣＫ上にある。
  共有点と２円の中心が
  　１直線上にあるので、
  　命題３ー６の補足により、
  ２円は
  　接する。
  
  　
  　
• もし
  　異なる２つの円ＡＢＣ、ＣＤＥが接するならば、
  　接点は唯一つである。
  　（以下、これを命題３ー６の補足６(接する２円の接点は１つ) という。）
  
  
  
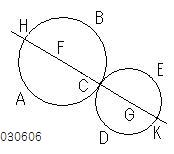
  命題３ー６の補足により、
  　それぞれの中心Ｆ、Ｇと接点は１直線上にあるので、
  　中心をとおる直線ＦＧと
  　　一方の円ＡＢＣが交わる点は
  　命題３ー２により、
  　２点Ｈ、Ｃだけである。
  背理法の仮定として、
  　他方の円ＣＤＥが
  　この２点Ｈ、Ｃともにおいて交わるとする。
  そうすると、
  　直径ＨＣが一致し、
  　したがって
  　中心が一致する。
  ところが、
  　命題の設定 命題３ー６により、
  　中心は一致しないから、
  　これは不可能である。
  背理法により、
  　他方の円が共有できるのは
  　１点Ｃだけである。
  よって、
  　接点は唯１つである。
  
• 命題３−６の補足(接する２円の接点と中心は１直線上)は推論用命題である。 　
  

  前提	作図	推論
  定義		1-15,1-16,3-3
  公準	1-2
  公理		1-3,1-8補2,1-7
  命題	3-1,3-2補	1-20
  その他		背理法、場合分け

  
  
• 命題３−６の補足２(中心は接線の接点での垂線上)は推論用命題である。 　
  

  前提	作図	推論
  定義		1-15,3-2
  公準
  公理
  命題	1-12	1-19
  その他		背理法

  
  
• 命題３−６の補足３(円周上から半径に垂直な直線は接線)は推論用命題である。 　
  

  前提	作図	推論
  定義		1-15,3-2
  公準	1-1,1-1補
  公理
  命題		1-19
  その他

  
  
• 命題３−６の補足４(円外の点から引いた接線は２本)は推論用命題である。 　
  

  前提	作図	推論
  定義		3-2
  公準	1-1,1-3
  公理
  命題	1-11,3-1,3-2補	1-4,1-7,1-8,1-20,1-47,3-6補3
  その他

  
  
• 命題３−６の補足５(接する２円の接点での接線は一致)は推論用命題である。 　
  

  前提	作図	推論
  定義
  公準
  公理		1-7補
  命題		1-14,3-6補,3-6補2,3-6補3
  その他		場合分け

  
  
• 命題３−６の補足６(接する２円の接点は１つ) は推論用命題である。 　
  

  前提	作図	推論
  定義
  公準
  公理
  命題		3-6,3-6補
  その他		背理法

• 命題３−６（円と接する円、直線）は推論用命題である。

  前提	作図	推論
  定義		1-15,3-3
  公準	1-1,1-1補
  公理		1-1,1-8
  命題	3-1,3-2補
  その他		背理法,コ2(題1-7)、場合分け

  
  

前 　　 次 　　 目次 　　頁頭