ユークリッド原論をどう読むか（２）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー１９（三角形の大きい辺と大きい角２）
　すべての三角形において
　大きい角には
　大きい辺が対する。

• 　三角形は、定義１ー１９の補足２による。
• 　大きいは公理１ー８による。
• 　角は、定義１ー９の補足による。
• 　辺は、定義１ー１９の補足による。

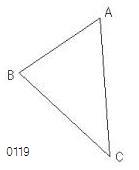
　ＡＢＣを
　角ＡＢＣが角ＢＣＡより大きい
　三角形
とせよ。

• 　△ＡＢＣ;∠ＡＢＣ＞∠ＢＣＡ
  をとっている。

　辺ＡＣも
　辺ＡＢより大きい
と主張する。

• 　ＡＣがＡＢに等しい場合
  　ＡＣがＡＢより小さい場合
  　ＡＣがＡＢより大きい場合
  　がある。
  
• 　公理１ー７の補足（等しい）
  による。

もし
　大きくない
ならば、

• 　背理法の仮定である。

　ＡＣは
　ＡＢに等しいか小さいかである。
　 ［等しい場合］
ところで
　ＡＣはＡＢに等しくない。

なぜなら［もし］
　《そう》［等しい
と］すれば

• 　英文では、'for then'となっているが、
  　推論の流れからは、'for if equals AB'と考えられる。
  
• 　「なぜならもし」については、
  　コメント（命題１ー４）を参照のこと。
• 一段階下の背理法の仮定である。

　角ＡＢＣも
　角ＡＣＢに等しくなる
であろう。

• 　英文では、'for then'となっているが、
  　推論の流れからは、'for if less than AB'と考えられる。
• 　命題１ー５（２等辺三角形の底角）
  による。
• 　∠ＡＢＣ＝∠ＡＣＢ
  となっている。

ところが
　そうではない。

• 　命題の仮定による。

したがって
　ＡＣはＡＢに等しくない。
　　　　　　【・・・(1)】

• 　一段階下の背理法による。

　［小さい場合］
また
　ＡＣはＡＢより小さくもない。

なぜなら
　そうすれば

「 　なぜならもし」については、
　コメント（命題１ー４）を参照のこと。
• 　再び一段階下の背理法の仮定である。

　角ＡＢＣも
　角ＡＣＢより小さくなる
であろう。

• 　命題１ー１８（三角形の大きい辺と大きい角１）
  による。
• 　∠ＡＢＣ＜∠ＡＣＢ
  となっている。

ところが
　そうではない。

• 　命題の仮定による。

したがって
　ＡＣはＡＢより小さくはない。

• 　一段階下の背理法による。

また
　等しくない
ことも先に証明された。

• 　(1) による。

ゆえに
　[３つの場合のうち
　２つの場合が不可能
だから ]
　ＡＣはＡＢより大きい。
よって
　すべての三角形において
　大きい角には大きい辺が対する。
　これが証明すべきことであった。

• 命題1-19は、
  命題1-19は、
  　△ＡＢＣ
  において
  　∠ＡＢＣ＞∠ＢＣＡ
  ならば、
  　ＡＣ＞ＡＢ
  のことである。
  
• 　ＡＢ上にない点Ｃから
  　垂線ＣＤと垂線でないＣＥがひかれたとすると、
  　命題１ー１７（三角形の２角の和）
  により、
  　角ＣＤＥ＞角ＣＥＤ
  となり、
  　本命題
  により、
  　ＣＥ＞ＣＤ
  となる。
  したがって、
  　 　直線上の点への直線外の点からの長さは、
  　垂線が最小である。
  　（以下、命題１ー１９の補足（垂線が最小） という。）

• 前提	作図	推論
  定義
  公準
  公理
  命題		1-17, 1-19
  その他

• 命題1-19は推論用命題である。
  

  前提	作図	推論
  定義
  公準
  公理		1-7補
  命題		1-5、1-18
  その他		場合分け、背理法、コ(題1-4)ft

前 　　 次 　　 目次 　　頁頭