ユークリッド原論をどう読むか（６）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論

第３巻

命題３ー２（弦は円の内部）　
(円内通過直線は円周と２交点)
もし
　円周上に
　任意の２点が
　とられるならば、
　２点を結ぶ線分は
　円の内部におちるであろう。

• 円周は定義１ー１７の補足による。
• 点は定義１ー１による。
• 線分は定義の補足（命題１ー１）による。
• 円の内部は定義１ー１６の補足２による。

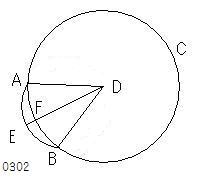
ＡＢＣを円とし、
　円周上に任意の２点Ａ、Ｂが
　とられたとせよ。

• 公準１ー１の補足により
  　円周上に２点Ａ、Ｂがとられ、
  　さらに
  　もう一点Ｃがいずれ取られるが、
  　これらを溯って用いて
  　円をＡＢＣとしている。

Ａ、Ｂを結ぶ線分は
　円の内部におちるであろう
　と主張する。

そうでないとすれば、

• 背理法の仮定である。

もし可能ならば

• 背理法の仮定により
  　一部は
  　外部におちるか
  　円周上におちる
  　場合がある。
  
• 「もし可能ならば」は、
  コメント２(命題１−７）参照のこと。

［ 一部が外部におちる場合は
　以下のようになる。］

• 場合分けである。

ＡＥＢのように
　［Ｅの部分が］
　外部におちるとし、

• ＡＢ間のすべてではなく
  　一部が外部におちている場合
  　が論理的には要求されている。

円ＡＢＣの中心がとられ、
　それをＤとし、 【・・・(a)】

• 中心Ｄを
  　作図により図中に取ることが
  　証明のために必須ではなく、
  　円の中心が
  　定義１−１５により
  　存在していることが
  　保証されているので、
  　命題３−１を前提としているわけではない。

ＤＡ、ＤＢが結ばれ、

• 公準１ー１による。

ＤＦＥがひかれたとせよ。

• 線分ＡＢ上で、
  　円の外部となる部分に
  　公準１ー１の補足により
  　点Ｅがとられ、
  　外部のＥと中心Ｄをむすぶと
  　交点が少なくとも１点あり、
  　それをＦとする。
  ＥはＡＢの中点とは限らない。

そうすればＤＡはＤＢに等しいから、

• (a) ,定義１ー１５による。

角ＤＡＥは角ＤＢＥに等しい。 【・・・(1)】

• 命題１ー５による。

そして
　三角形ＤＡＥの１辺ＡＥ［がＡＥ］Ｂ≪が≫［に］
　延長されたから、
　角ＤＥＢは角ＤＡＥより大きい。

• 命題１ー１６による。

しかも
　角ＤＡＥは
　角ＤＢＥに等しい。

• (1) による。

それゆえ
　角ＤＥＢは
　角ＤＢＥより大きい。

• 公理１ー８の補足２による。

ところが
　大きい角には大きい辺が対する。

• 命題１ー１９による。

ゆえに
　ＤＢは
　ＤＥより大きい。
そして
　ＤＢは
　ＤＦに等しい。

• 定義１ー１５による。

したがって
　ＤＦはＤＥより、
　すなわち
　小さいものが
　大きいものより大きい。

• 公理１ー８の補足２による。

これは不可能である。 ゆえに
　ＡＢを結ぶ線分は
　円の外部に［一部が］おちないであろう。

• 一部が外部におちる場合の
  　背理法はここで終わる。

［ 円周上におちる場合は
　以下のようになる。］
同様にして
　円周そのものの上にもおちない
　ことを証明しうる。

• Ｅが円周上にある場合は、
  　ＥとＦが一致し、
  　同様に
  　角ＤＥＢがＤＢＥより大きく、
  　ＤＢがＤＥより大きくなるはずだが、
  　ＤＢ、ＤＥはともに半径だから、
  　ＤＢはＤＥに等しくなり、
  　小さいものが
  　大きいものに等しくなるから、
  　矛盾する。

［したがって
　２つの場合の結果から
　内部に落ちる以外は不可能であるとわかった。

よって
　もし
　円周上に任意の２点がとられるならば、
　２点を結ぶ線分は
　円の内部におちるであろう。
　
これが証明すべきことであった。

• 「線分が内部におちる」ということは
  　「線分のすべての部分が内部におちる」
  　ということで、
  　その否定は
  　「線分の一部が外部または周上におちる」
  　ことである。
• 証明は
  　Ｅの部分が
  　外部または周上にあれば有効である。
  線分の全体が
  　外に出ている必要はない。
• 背理法を用いなくても、
  
  
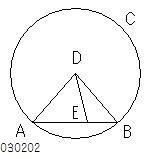
  　ＡＢの間にあるＥについては、
  　上記論証中にあるように
  　命題１ー１９により
  　ＤＥは半径ＤＢより小さいから、
  　定義１−１６の補足２により
  　円の内部にある
  　ことが論証できる。
• 円の内部を通る直線は
  　円周と２点で交わる。
  また、
  　内部の点から外部に向かう半直線は
  　円周と１点で交わる。
  　（以下、これを「命題３−２の補足」(円内通過直線は円周と２交点)という。）
  これは以下のように証明される。
  命題の補足３（定義１ー１４）により、
  　円の内部を通る直線は
  　少なくとも２点で円周と交わり、
  　本命題により
  　円周上の２点を結ぶ線分は
  　両端を除いて円の内部であるから
  　円周と交わる点は２点である。
  したがって、
  　内部の点から外部に向かう半直線は
  　円周と１点で交わる。
  　
• 命題３ー２は推論用命題である。

  前提	作図	推論
  定義		1-15,1-16補2
  公準	1-1,1-1補
  公理		1-8補2
  命題		1-5,1-16,1-19
  その他		背理法,コ2(題1-7)、場合分け

• 命題３−２の補足は作図用命題である。

  前提	作図	推論
  定義
  公準
  公理
  命題	補3(義1-14)	3-2
  その他

前 　　 次 　　 目次 　　頁頭