ユークリッド原論をどう読むか（２）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー２０（三角形の２辺の和と１辺）
　すべての三角形において
　どの２辺をとって
も
　その和は残りの１辺より大きい。

• 　三角形は、定義１ー１９の補足２による。
• 　辺は、定義１ー１９の補足による。
• 　大きいは、公理１ー８による。

　ＡＢＣを三角形
とせよ。

• 　△ＡＢＣ
  をとっている。

　三角形ＡＢＣのどの２辺をとっても
　その和は残りの１辺より大きい、
すなわち
　ＢＡ、ＡＣの和はＢＣより、
　ＡＢ、ＢＣの和はＡＣより、
　ＢＣ、ＣＡの和はＡＢより
　大きい
と主張する。

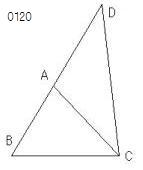
　ＢＡが点Ｄまで延長され、
　ＡＤがＣＡに等しくされ、

• 　公準１ー２（作図.直線の延長）、
  　命題１ー３（作図・等しい線分を切り取る）
  による。
• 　点Ｄ(延長ＢＡ;;ＡＤ＝ＣＡ)
  をとっている。 　

　ＤＣが結ばれた
とせよ。
　　　　　　【・・・(a)】

• 　公準１ー１（作図.直線）
  による。
• 　線分(Ａ,Ｄ)
  をとっている。

そうすれば
　ＤＡはＡＣに等しい

• 　(a) による。
• 　ＤＡ＝ＡＣ
  となっている。

から、
　角ＡＤＣもＡＣＤに等しい。

• 　命題１ー５（２等辺三角形の底角）
  による。
• 　∠ＡＤＣ＝∠ＡＣＤ
  となっている。

それゆえ
　角ＢＣＤは角ＡＤＣより大きい。

• 　(a) ,
  　公理１ー８の補足２（等より大・小、大・小に等）
  による。
• 　∠ＢＣＤ＞∠ＡＤＣ
  となっている。

そして
　ＤＣＢは角ＢＣＤが
　角ＢＤＣより大きい三角形であり、
　大きい角には大きい辺が対する
から、
　ＤＢはＢＣより大きい。

• 　命題１ー１９（三角形の大きい辺と大きい角２）
  による。
• 　ＤＢ＞ＢＣ
  となっている。

ところが
　ＤＡはＡＣに等しい。

• 　(a) による。
• 　ＤＡ＝ＡＣ
  となっている。

ゆえに
　ＢＡ、ＡＣの和はＢＣより大きい。

• 　公理１ー８の補足２（等より大・小、大・小に等）
  による。
• 　ＢＡ＋ＡＣ＞ＢＣ
  となっている。

同様にして、
　ＡＢ、ＢＣの和もＣＡより、
　ＢＣ、ＣＡの和もＡＢより
　大きい
ことを証明しうる。
よって
　すべての三角形において
　どの２辺をとって
も
　その和は残りの１辺より大きい。
　これが証明すべきことであった。

• 命題1-20は。
  　△ＡＢＣ
  において、
  　ＢＡ＋ＡＣ＞ＢＣ、
  　ＡＢ＋ＢＣ＞ＡＣ、
  　ＢＣ＋ＣＡ＞ＡＢ
  のことである。
  
• 命題1-20は推論用命題である。

  前提	作図	推論
  定義
  公準	1-1、1-2
  公理		1-8補2
  命題	1-3	1-5、1-19
  その他

前 　　 次 　　 目次 　　頁頭