ユークリッド原論をどう読むか(6)
頁末
前
次
目次
ユークリッド原論
第3巻
命題3ー5(交わる2円の中心)
(2円の交点は2つ)
もし
二つの円が
互いに交わるならば、
それらは
同じ中心をもたないであろう。
2円ABC、CDGが
点B、Cにおいて
互いに交わるとせよ。
それらは
同じ中心をもたないであろう
と主張する。
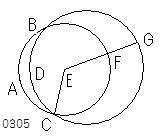
- 円ABCがあり、
もう一つの円が
ABCに交わるのであるから、
定義1−8の補足により
ABCの円周上に交点Cがあり、
もう一つの円の周を
ABCの外部の方に後戻りせずに進むと、
定義1ー8の補足により
円は
ABCの外部と内部にまたがっているので、
いずれ内部に入り、
さらに進むと元の点に戻る。
内部に入るときに
円ABCと、
Cとは別の交点Bをもつ。
溯ってB、Cを用いている。
ここでは少なくとも
2点で交わっていると主張している。
2点しかないというのではない。
[......(A)]
もし可能ならば、
同じ中心をEとし、
【・・・(a)】
- 「Eをとり(take the center E)」と表現せずに、
「Eとし(let it be E)」と表現している
ことに注目すべきである。
(英文は、
Euclid's Elements
Clark University Professor D.E.Joyceの
http://aleph0.clarku.edu/~djoyce/java/elements/elements.html)
による。)
実際に作図でEを取ることを
しているのではなく、
論理的に存在を確保されている
中心を
Eとしているのである。
ECが結ばれ、
任意にEFGがひかれたとせよ。
- 命題の仮定により
円CDGは
円ABCの内部と外部分かれる。
公準1ー1の補足により
外部の円周上に点Gをとり、
公準1ー1によりEGを結ぶ。
EGは
円ABCの内部と外部を結ぶ線分であるから、
命題3−2の補足により
ABCの円周と交点をもつ。
この交点をFとする。
【・・・(b)】
そうすれば
点Eは
円ABCの中心であるから、
ECはEFに等しい。
【・・・(1)】
また
Eは
円CDGの中心でもあるから、
ECはEGに等しい。
しかも
ECがEFに等しい
ことも先に証明された。
それゆえ
EFもEGに、
すなわち
小さいものが大きいものに等しい。
これは不可能である。
ゆえに
点Eは
円ABC、CDGの中心ではない。
よってもし
二つの円が
互いに交わるならば、
それらは
同じ中心をもたないであろう。
これが証明すべきことであった。
- この命題の証明には、
第3巻のこれ以前の命題を
前提としていない。
- 二つの円が
交わるとき
二つの円周は
ただ2点で交わる。
(以下、これを命題3−5の補足(2円の交点は2つ)という。)
これは
以下のように証明される。
少なくとも2点で交わることは
上の証明中の解説(A)に述べている。
もし
3点B、C、Hで交われば、
命題3−1により
2円の中心は、
線分BCの垂直2等分線上にあり、
また
線分CHの垂直2等分線上にある。
命題1ー30の補足により
交わる2線分の
二つの垂線は
交わるので、
その交点をKとすると、
Kは
2円の中心となるが、
これは命題3−5に矛盾する。
したがって、
二つの円が交わるとき
二つの円周は
ただ2点で交わる。
-
命題3−5の補足(2円の交点は2つ)
- 命題3−5は推論用命題である。
前
次
目次
頁頭
