ユークリッド原論をどう読むか（１０）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第６巻

命題６ー１０（作図.線分の区分）
（区分線分の端点共有化）, 線分比による内分・外分, (作図.線分比による線分の内分点・外分点)
与えられた、
　分けられていない線分を、
　与えられた、
　分けられている線分と
　同様に分けること。

• 線分は、 定義の補足（命題１ー１） による。

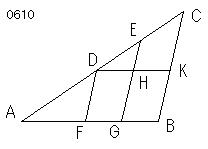
与えられた、
　分けられていない線分をＡＢとし、
　ＡＣを
　点Ｄ、Ｅにおいて分けられている線分とし、
　それらが
　任意の角をはさむようにし、

• 端点を共有しない場合は
  　以下のように考える。
  分けられた線分を
  　Ａ'Ｄ'Ｅ'Ｃ'とする。
  公準１ー１の補足（作図.任意の点をとる）
  により、
  　直線ＡＢ上でないところに点Ｃ"をとり、
  　公準１ー１（作図.直線）
  により、
  　Ａから半直線ＡＣ"をひく。
  命題１ー３の補足（作図.等しい線分となる点）
  により、
  　半直線ＡＣ"上にＤ、Ｅ、Ｃをとり、
  　線分ＡＤ、ＤＥ、ＥＣが
  　Ａ'Ｄ'、Ｄ'Ｅ'、Ｅ'Ｃ'に
  　等しくなるようにする。
  こうすることで、
  　 端点を共有しない２線分ＡＢ、Ａ'Ｃ'を、
  　端点Ａを共有するＡＢ、ＡＣと
  　することができる。 （以下、命題６ー１０の補足 （区分線分の端点共有化）という。）
• 　ＡＢ、ＡＣ
  に対して、
  　Ｄ[ＡＣ]、
  　Ｅ[ＤＣ]
  をとっている。

　ＣＢが結ばれ、

• 公準１ー１（作図.直線）
  による。
• 　線分ＣＢ
  をとっている。

　 Ｄ、Ｅを通り
　ＢＣに平行に
　ＤＦ、ＥＧがひかれ、 【・・・(a)】

• 命題１ー３１（作図・平行線）
  による。
  ＤＦ、ＥＧについて、
  　Ａは辺ＢＣと反対の側にあるから、
  　命題１ー３０の補足(交線に平行な線)
  により、
  　ＤＦ、ＥＧは辺ＡＢと１点で交わる。
  その交点を改めてＦ、Ｇとし、
  　溯って用いている。
• 　Ｆ(ＡＢ;;ＢＣ‖ＤＦ)、
  　Ｇ(ＡＢ;;ＢＣ‖ＥＧ)
  をとっている。

　Ｄを通り
　ＡＢに平行に
　ＤＨＫがひかれたとせよ。

• 命題１ー３１（作図・平行線）
  による。
  ＤＨＫについて、
  　Ｃは辺ＡＢと反対の側にあるから、
  　命題１ー３０の補足(交線に平行な線)
  により、
  　ＤＨＫは辺ＥＧ、ＣＢと１点で交わる。
  その交点を改めてＨ、Ｋとし、
  　溯って用いている。
• 　Ｋ(ＢＣ;;ＤＫ‖ＡＢ)、
  　交点Ｈ(ＤＫ,ＥＧ)
  をとっている。

そうすれば
　ＦＨ、ＨＢの双方は
　平行四辺形である。

• 定義の補足（命題１ー３４）(平行四辺形・対角線)
  による。
• 　ＦＨ;平四(ＦＧ,ＤＨ)、
  　ＨＢ;平四(ＧＢ,ＨＫ)
  となっている。

それゆえ
　 ＤＨはＦＧに、
　ＨＫはＧＢに等しい。 【・・・(b)】

• 命題１ー３４（平行四辺形の対辺・対角・対角線）
  による。
• 　ＤＨ＝ＦＧ、
  　ＨＫ＝ＧＢ
  となっている。

そして
　線分ＨＥは
　三角形ＤＫＣの１辺ＫＣに平行にひかれたから、

• (a) による。
• 　ＨＥ‖ＫＣ
  となっている。

　比例し、
　ＣＥがＥＤに対するように、
　ＫＨがＨＤに対する。

• 命題６ー２（三角形の辺の平行線による辺の比例区分）
  による。
• 　ＣＥ：ＥＤ＝ＫＨ：ＨＤ
  となっている。

ところが
　ＫＨはＢＧに、
　ＨＤはＧＦに等しい。

• (b)による。
• 　ＫＨ＝ＢＧ、
  　ＨＤ＝ＧＦ
  となっている。

ゆえに
　ＣＥがＥＤに対するように、
　ＢＧがＧＦに対する。 【・・・(1)】

• 命題５ー１１の補足２（等しい量は同じ比をもつ）、
  定義５ー６（比例）
  による。
• 　ＣＥ：ＥＤ＝ＢＧ：ＧＦ
  となっている。

また
　ＦＤは
　三角形ＡＧＥの１辺ＧＥに平行《にひかれた》［である］から、

• (a), 命題１ー３０（平行の平行）
  による。
• 　ＦＤ‖ＧＥ
  となっている。

　比例し、
　ＥＤがＤＡに対するように
　ＧＦがＦＡに対する。

• 命題６ー２（三角形の辺の平行線による辺の比例区分）
  による。
• 　ＥＤ：ＤＡ＝ＧＦ：ＦＡ
  となっている。

ところが
　ＣＥがＥＤに対するように、
　ＢＧがＧＦに対することが
　先に証明された。

• (1) による。
• 　ＣＥ：ＥＤ＝ＢＧ：ＧＦ
  となっている。

したがって
　ＣＥがＥＤに対するように、
　ＢＧがＧＦに対し、
　ＥＤがＤＡに対するように、
　ＧＦがＦＡに対する。

• 　ＣＥ：ＥＤ＝ＢＧ：ＧＦ、
  　ＥＤ：ＤＡ＝ＧＦ：ＦＡ
  となっている。

よって
　与えられた、
　分けられていない線分ＡＢを、
　与えられた線分ＡＣと同様に分けられた。
これが作図すべきものであった。

• 命題６ー１０は、
  　ＡＢ、ＡＣ
  に対して、
  　Ｄ[ＡＣ]、
  　Ｅ[ＤＣ]、
  　Ｆ(ＡＢ;;ＢＣ‖ＤＦ)、
  　Ｇ(ＡＢ;;ＢＣ‖ＥＧ)
  をとれば、
  　ＣＥ：ＥＤ＝ＢＧ：ＧＦ、
  　ＥＤ：ＤＡ＝ＧＦ：ＦＡ
  のことである。
• 　　線分ＡＢ上に
  　点Ｃが
  　　ある
  とき、
  　Ｃは、
  　　ＡＢをＡＣ：ＣＢに内分
  　　　する
  といい、
  　Ｂは、
  　　ＡＣをＡＢ：ＢＣに外分
  　　　する
  という。
  (以下、定義の補足２（命題６ー１０） (線分比による内分・外分)という。)
  
• 　線分ＡＢが
  　　ＡＣ：ＣＢに内分
  　　　され、
  　　ＡＣ＞ＣＢ
  　　　となる
  とき、
  　　ＡＢをＡＣ：ＣＢに外分
  　　　する
  　　点Ｄを
  　　　とることができる。
  また、
  　線分ＡＢが
  　　ＡＤ：ＤＢに外分
  　　　されている
  とき、
  　　ＡＢをＡＤ：ＤＢに内分
  　　　する
  　　点Ｃを
  　　　とることができる。
  (以下、命題６ー１０の補足３ (作図.線分比による線分の内分点・外分点)という。)
  　ＡＢが
  　　Ｃで内分
  　　　され
  　　ＡＣ＞ＢＣ
  　　　となる
  とき、
  　命題１ー３（作図・等しい線分を切り取る）
  により、
  　　Ｅ（ＡＣ；ＥＣ＝ＣＢ）を
  　　　とり、
  　命題６ー２の補足（作図.比例第４項）
  により、
  　　ＡＢ：Ｇ＝ＡＥ：ＥＣ
  　　　となるように、
  　　Ｇを
  　　　とり、
  　命題１ー３（作図・等しい線分を切り取る）
  により、
  　　Ｄ（延長ＡＢ；ＤＢ＝Ｇ）
  　　　をとれ
  ば、
  　Ｄは、
  　　ＡＢをＡＣ：ＣＢに外分
  　　　する。
  なぜなら、
  　命題５ー１８（比例ならば合比も比例）
  により、
  　ＡＤ：ＤＢ＝ＡＣ：ＥＣ
  　　となり、
  　命題５ー７（同一量の比）
  により、
  　ＡＢ：ＤＢ＝ＡＣ：ＢＣ
  となる。
  また、
  　ＡＢが
  　　Ｄで外分
  　　　される
  とき、
  　命題１ー３（作図・等しい線分を切り取る）
  により、
  　　Ｆ（延長ＡＢ；ＦＤ＝ＢＤ）を
  　　　とり、
  　命題６ー１０（作図.線分の区分）
  により、
  　　ＡＣ：ＣＢ＝ＡＤ：ＤＦ
  　　　となるように、
  　　Ｃを
  　　　とれ
  ば、
  　Ｃは、
  　　ＡＢをＡＤ：ＢＤに内分
  　　　する。
  なぜなら、
  　命題５ー７（同一量の比）
  により、
  　　ＡＣ：ＣＢ＝ＡＤ：ＤＢ
  　　　　となる。
• 命題６ー１０の補足 （区分線分の端点共有化）

  前提	作図	推論
  定義
  公準	1-1,1-1補
  公理
  命題	1-3補
  その他

• 命題６ー１０の補足３ (作図.線分比による線分の内分点・外分点)

  前提	作図	推論
  定義		補2(題6-10)
  公準
  公理
  命題	1-3,6-2補,6-10	5-7,5-18
  その他

• 命題６ー１０は作図用命題である。

  前提	作図	推論
  定義		補(題1-34),5-6
  公準	1-1,1-1補
  公理
  命題	1-3補,1-30,1-30補,1-31	1-34,5-11補2,6-2
  その他

前 　　 次 　　 目次 　　頁頭