ユークリッド原論をどう読むか(9518)
頁末
前
次
目次
ユークリッド原論
第5巻
命題5ー18(比例ならば合比も比例)
もし
量が
分割比によって[得られた]比例する[量]
ならば、
合比によっても
比例するであろう。
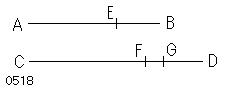
AE、EB、CF、FDを
分割比によって[得られた]比例する量とし、
AEがEBに対するように、
CFがFDに対するとせよ。
-
同じ比をもつ線分の作図(仮想的)は、
コメント2(命題5ー4)参照のこと。
-
AB、CD
に対して、
点E[AB]、
点F(CD;;AE:EB=CF:FD)
をとっている。
それらは
合比によっても比例し、
ABがBEに対するように、
CDがFDに対するであろう
と主張する。
もし
ABがBEに対するように、
CDがDFに対するのでなければ、
ABがBEに対するように、
CDがDFより
小さいものに対するか、
あるいは
大きいものに対するか
であろう。
まず、
小さいDGに対するとせよ。
【・・・(a
)】
- 場合分け(1)である。
-
点G(CD;;AB:BE=CD:DG,DG<DF)
としている。
そうすれば
ABがBEに対するように、
CDがDGに対するから、
- (a)
による。
-
AB:BE=CD:DG
となっている。
それらは合比によって比例する量である。
それゆえ
分割比によっても比例するであろう。
- 命題5ー17(合比で比例なら分割比でも比例)
のことである。
ゆえに
AEがEBに対するように、
CGがGDに対する。
- 命題5ー17(合比で比例なら分割比でも比例)
による。
-
AE:EB=CG:GD
となっている。
ところが
AEがEBに対するように、
CFがFDに対することが仮定される。
- 命題の設定
である。
-
AE:EB=CF:FD
となっている。
ゆえに
CGがGDに対するように、
CFがFDに対する。
- 命題5ー11(同一の比に同じ比)
による。
-
CG:GD=CF:FD
となっている。
ところが
第1のCGは第3のCFより大きい。
したがって
第2のGDも第4のFDより大きい。
- 命題5ー14(同じ比の前(後)項の大等小)
による。
-
GD>FD
となっている。
しかも
小さくもある。
これは不可能である。
それゆえ
ABがBEに対するように、
CDがFDより小さいものに対することはない。
[
大きいものに対するとしても、]
同様にして
大きいものに対することもない
ことを証明しうる。
-
場合分け(2)のことで、
これも背理法による。
-
点G(CD;;AB:BE=CD:DG,DG>DF)
をとると、
命題5ー17(比例なら分割比も比例)
により、
AE:EB=CG:GD
ところが、
命題の設定
により、
AE:EB=CF:FD
よって、
命題5ー11(同一の比に同じ比)
により、
CG:GD=CF:FD
点Gの取り方
により
CG<CF
命題5ー14(同じ比の前(後)項の大等小)
により
GD<FD
ところが、
点Gの取り方
により
GD>FD
であった。
よって、
矛盾が生じ、
背理法
により
GD>FDでない。
したがって
[
2つの場合の結果により、]
FDそのものに対する。
よってもし
量が
分割比によって[得られた]比例する[量]
ならば、
合比によっても
比例するであろう。
これが証明すべきことであった。
-
命題5ー17(比例ならば分割比も比例)
の表現に合わせている。
- 命題5ー18は、
A:B=C:D
ならば
(A+B):B=(C+D):D
のことである。
- 命題5ー18は推論用命題である。
前
次
目次
頁頭
