ユークリッド原論をどう読むか（１０）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第６巻

命題６ー１１（作図.比例第３項）
与えられた２線分に対し
　第３の比例項を見いだすこと。

• 線分は、 定義の補足（命題１ー１） による。
• 比例は、 定義５ー６ による。
• 項は、 定義５ー８の補足 による。

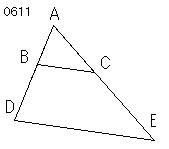
与えられた線分をＢＡ、ＡＣとし、
　それらが
　任意の角をはさむようにせよ。

• 命題６ー１０の補足（区分線分の端点共有化）
  による。
• 　線分ＢＡ、ＡＣ
  をとっている。

このとき
　ＢＡ、ＡＣに対し
　第３の比例項を見いださねばならぬ。
　
点Ｄ、ＥＤまで延長されたとし、

• 公準１ー２（作図.直線の延長）
  による。

　 ＢＤがＡＣに等しくされ、 【・・・(a)】

• 命題１ー３の補足（作図.等しい線分となる点）
  により、
  　点Ｄをとり溯って用いている。
• 　Ｄ(延長ＡＢ;;ＢＤ＝ＡＣ)
  となっている。

　ＢＣが結ばれ、

• 公準１ー１（作図.直線）
  による。
• 　線分ＢＣ
  をとっている。

　 Ｄを通り
　ＢＣに平行にＤＥがひかれたとせよ。 【・・・(b)】

• 命題１ー３１（作図・平行線）
  により
  　ＢＣに平行にＤＥ'をひく。
  命題１ー３０の補足(交線に平行な線)
  により、
  　ＤＥ'はＡＥと交わる。
  その交点を改めてＥとし、
  　溯って用いている。
• 　Ｅ(延長ＡＣ;;ＢＣ‖ＤＥ)
  をとっている。

そうすれば
　ＢＣは
　　三角形ＡＤＥの１辺ＤＥに
　　平行《にひかれた》［である］から、

• (b)による。

　比例し、
　ＡＢがＢＤに対するように、
　ＡＣがＣＥに対する。

• 命題６ー２（三角形の辺の平行線による辺の比例区分）
  による。
• 　ＡＢ：ＢＤ＝ＡＣ：ＣＥ
  となっている。

ところが
　ＢＤはＡＣに等しい。

• (a)による。
• 　ＢＤ＝ＡＣ
  となっている。

したがって
　ＡＢがＡＣに対するように、
　ＡＣがＣＥに対する。

• 命題５ー１１の補足２（等しい量は同じ比をもつ）、
  命題５ー１１（同一の比に同じ比）
  による。
• 　ＡＢ：ＡＣ＝ＡＣ：ＣＥ
  となっている。

よって
　２線分ＡＢ、ＡＣが与えられたとき、
　それらに対し
　第３の比例項ＣＥが見いだされた。
これが作図すべきものであった。

• 命題６ー１１は、
  　ＡＢ、ＡＣ
  に対し、
  　Ｄ(半直線ＡＢ;;ＢＤ＝ＡＣ)、
  　Ｅ(半直線ＡＣ;;ＤＥ‖ＢＣ)
  をとれば、
  　ＡＢ：ＡＣ＝ＡＣ：ＣＥ
  のことである。
  
  
• 命題６ー１１は作図用命題である。

  前提	作図	推論
  定義
  公準	1-1,1-2
  公理
  命題	1-3補,1-30補 ,1-31 ,6-10補	5-11,5-11補2,6-2
  その他

前 　　 次 　　 目次 　　頁頭