ユークリッド原論をどう読むか（１４）
頁末 　　 前 　　 次 　 目次

ユークリッド原論

第１０巻
　
命題１０ー８２（劣線分に付加して全体と、平方で非通約、平方和が有理面積、全体と中項面積をかこむ線分は唯一）
　劣線分には
　　それに付加
　　　されて
　　全体と平方において通約
　　　できず、
　　それらすなわち全体と
　　付加された線分と
　　の上の正方形の和を
　　　有理面積とし、
　　それらによってかこまれる矩形の２倍を
　　　中項面積とする
　　ただーつの線分が
　　　ある。

• 劣線分は、
  定義の補足（命題１０ー７６）による。
• 平方において通約は、
  定義１０ー２による。
• 線分は、
  定義の補足（命題１ー１）による。
• 正方形は、
  定義１ー２２による。
• 有理面積は、
  定義１０ー４の補足による。
• 矩形は、
  定義１ー２２による。
• 倍は、
  定義の補足（公理１ー５）による。
• 中項面積は、
  定義の補足２（命題１０ー２３）による。

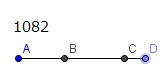
　　ＡＢを
　　　劣線分とし、
　　ＡＢに
　ＢＣが
　　　付加された
とせよ。
そうすれば
　ＡＣ、ＣＢは
　　平方において通約
　　　できず、
　　それらの上の正方形の和を
　　　有理面積とし、
　　それらによってかこまれる矩形の２倍を
　　　中項面積とする。

• 　命題１０ー３３（作図.２線分；平方で非通約、平方和が有理面積、矩形が中項面積）
  により、
  　　　２線分をとり、
  　　　大きい方をＡＣ、
  　　　小さい方をＢＣ
  とし、
  　命題１ー３（作図・等しい線分を切り取る）　
  により、
  　　　Ｂ’（ＡＣ；Ｂ’Ｃ＝ＢＣ）
  　　をとり、
  　　　改めて、
  　　　Ｂ’をＢ
  　　とする。
  
• 　ＡＢ；劣線分
  　　ＡＣ¬∩^2 ＢＣ、
  　　正方(_ＡＣ)＋正方(_ＢＣ)；有理面積
  　　矩形(ＡＣ、ＢＣ)；中項面積
  　　ＡＣ＞ＢＣ
  となっている。

　ＡＢには
　　同じ条件を満たす他のいかなる線分も
　　　付加されない
と主張する。

もし
可能ならば、
　ＢＤが
　　付加された
とせよ。

• 　背理法の仮定である。
• 　ＡＢ；劣線分
  　　ＡＤ¬∩^2 ＢＤ、
  　　正方(_ＡＤ)＋正方(_ＢＤ)；有理面積
  　　矩形(ＡＤ、ＢＤ)；中項面積
  　　ＡＤ＞ＢＤ
  となっている。

そうすれば
　ＡＤ、ＤＢは
　　平方において通約
　　　できず
　　上述の条件を
　　　みたす。

• 　ＡＢ；劣線分
  　　ＡＤ¬∩^2 ＢＤ、
  　　正方(_ＡＤ)＋正方(_ＢＤ)；有理面積
  　　矩形(ＡＤ、ＢＤ)；中項面積
  　　ＡＤ＞ＢＤ
  となっている。

そして
　　ＡＤ、ＤＢ上の正方形の和と
　　ＡＣ、ＣＢ上の正方形の和と
　の差は
　　矩形ＡＤ、ＤＢの２倍と
　　矩形ＡＣ、ＣＢの２倍との差
　　　に等しく、

• 　命題の設定、
  背理法の設定
  　命題２ー７（差の平方）
  により、
  　正方(_ＡＤ)＋正方(_ＤＢ)ー２矩形(ＡＤ、ＤＢ)
  　＝正方(_ＡＣ)＋正方(_ＣＢ)ー２矩形(ＡＣ、ＣＢ)
  　＝正方(_ＡＢ)
  による。
  
• 　正方(_ＡＤ)＋正方(_ＤＢ)ー（正方(_ＡＣ)＋正方(_ＣＢ)）
  　＝２矩形(ＡＤ、ＤＢ)ー２矩形(ＡＣ、ＣＢ)
  となっている。

　　ＡＤ、ＤＢ上の正方形の和と
　　ＡＣ、ＣＢ上の正方形の和と
　の差は
　　　有理面積である、
なぜなら
　両方とも
　　　有理面積である
から。

• 　命題の設定、
  　背理法の仮定、
  　定義１０ー４の補足（有理面積、無理面積）
  　命題１０ー１５（通約量はその和・差とも通約）
  による。
• 　「なぜなら」は、
  　コメント２（命題１ー１６）
  参照のこと。
• 　　正方(_ＡＤ)＋正方(_ＤＢ)ー（正方(_ＡＣ)＋正方(_ＣＢ)
  　　　；有理面積
  となっている。

したがって
　矩形ＡＤ、ＤＢの２倍は
　　矩形ＡＣ、ＣＢの２倍より
　　有理面積だけ
　　　大きい。

• 　前節、前々節、
  　定義１０ー４の補足（有理面積、無理面積）
  による。
• 　２矩形(ＡＤ、ＤＢ)ー２矩形(ＡＣ、ＣＢ)；有理面積
  となっている。

これは不可能である。
なぜなら
　両方とも
　　　中項面積である
から。

• 　命題の設定、
  背理法の仮定、
  　命題１０ー２６（中項面積の差は無理面積）
  による。
  

よって
　劣線分には
　　それに付加されて
　　全体と平方において通約
　　　できず、
　　それらの上の正方形の和を
　　　有理面積とし、
　　それらによってかこまれる矩形の２倍を
　　　中項面積とする
　ただ一つの線分が
　　　ある。

• 　前節、背理法による。
• 　ＡＢ；劣線分
  　　ＡＣ¬∩^2 ＢＣ、
  　　正方(_ＡＣ)＋正方(_ＢＣ)；有理面積
  　　矩形(ＡＣ、ＢＣ)；中項面積
  　　ＡＣ＞ＢＣ
  　　　となる
  　ＢＣは
  　　唯一である。

これが証明すべきことであった。

• 命題１０ー８２は、
  　命題１０ー３３（作図.２線分；平方で非通約、平方和が有理面積、矩形が中項面積）
  により
  　ＡＣ、ＢＣ
  　　ＢＣ¬∩^2 ＡＣ
  　　正方(_ＡＣ)＋正方(_ＣＢ)；有理面積、
  　　矩形(ＡＣ、ＣＢ)；中項面積、
  　　ＡＢ；ＡＣーＢＣ、劣線分
  をとり、
  　ＡＤ、ＢＤ
  　　ＢＤ¬∩^2 ＡＤ
  　　正方(_ＡＤ)＋正方(_ＤＢ)；有理面積、
  　　矩形(ＡＤ、ＤＢ)；中項面積、
  ならば、
  　　ＢＤ＝ＢＣ
  のことである。
• 命題１０ー８２は推論用命題である。

  前提	作図・構成	推論
  定義		10-4補
  公準
  公理
  命題	1-3,10-33	2-7,10-15,10-26
  その他		コ2(題1-16), 背理法

前 　　 次 　　 目次 　　頁頭