ユークリッド原論をどう読むか（５）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論

第２巻

命題２ー７（差の平方）
もし
　線分が
　任意に２分されるならば、
　全体の上の正方形と
　一つの部分の上の正方形との
　和は
　全体の線分と
　この部分とに
　かこまれた矩形の２倍と
　残りの部分の上の正方形との
　和に等しい。

• 線分は、定義の補足（命題２ー１）による。
• 直線は、定義１ー４による。
• かこまれたは、定義２ー１による。
• 矩形は、定義１ー２２による。
• 倍は、定義の補足（公理１ー５）による。
• 正方形は、定義１ー２２による。
• 等しいは、公理１ー７による。

線分ＡＢが
　点Ｃにおいて
　任意に分けられたとせよ。

• 　線分ＡＢ、
  　点Ｃ[ＡＢ]
  をとっている。

ＡＢ、ＢＣ上の正方形の和は
　ＡＢ、ＢＣにかこまれた矩形の２倍と
　ＣＡ上の正方形との
　和に等しい
　と主張する。
　


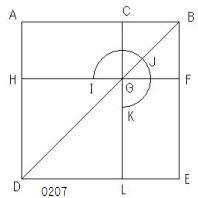
ＡＢ上に
　正方形ＡＤＥＢが描かれたとし、

• 命題１ー４６（作図.線分上に正方形）
  による。
• 　正方ＡＤＥＢ(_ＡＢ)
  をとっている。

そして
　作図がなされたとせよ。

• 公準１ー１（作図.直線）
  により
  　対角線ＢＤをひき、
  　命題１ー３１（作図・平行線）
  により
  　Ｃを通り
  　ＢＥに平行な直線をひくと、
  　ＢＥはＢＤ、ＥＤと交わっているから、
  　命題１ー３０の補足(交線に平行な線)
  により
  　この直線とＢＤ、ＥＤとは交わり、
  　その交点を、それぞれＧ、Ｌとする。
  命題１ー３１（作図・平行線）
  により
  　Ｇを通り
  　ＡＢに平行な直線をひくと、
  　ＡＢはＡＤ、ＢＥと交わっているから、
  　命題１ー３０の補足(交線に平行な線)
  により
  　この直線とＡＤ、ＢＥとは交わり、
  　その交点を、それぞれＨ、Ｆとする。
  グノーモーンをＩＪＫとする。
  　この命題以降、
  　この部分を原論は省略している。
• 　線分ＢＤ、
  　交点Ｇ(平行線(Ｃ,ＢＥ),ＢＤ)、
  　交点Ｌ(平行線(Ｃ,ＢＥ),ＥＤ)、
  　交点Ｈ(平行線(Ｇ,ＡＢ),ＡＤ)、
  　交点Ｆ(平行線(Ｇ,ＡＢ),ＢＥ)、
  　グＩＪＫ
  をとっている。

そうすれば
　［矩形］ＡＧはＧＥに等しいから、

• 命題１ー４３（平行四辺形の補形）
  による。
• 　矩形(ＡＧ)＝矩形(ＧＥ)
  　　　　　　【・・・(1)】

双方に
　［矩形］ＣＦが加えられたとせよ。
そうすれば
　ＡＦ全体はＣＥ全体に等しい。

• 公理１ー２（等しいものに等しいものを加える）、
  　公理１ー１の補足（等しいものに等しい）
  による。
• (1) より、
  　矩形(ＡＧ)＋矩形(ＣＦ)
  　＝矩形(ＧＥ)＋矩形(ＣＦ)
  よって
  　矩形(ＡＦ)＝矩形(ＣＥ)　
  　　　　　　【・・・(2)】

ゆえに
ＡＦ、ＣＥの和は
　ＡＦの２倍である。

• 公理１ー２（等しいものに等しいものを加える）
  による。
• (2) より、
  　矩形(ＡＦ)＋矩形(ＣＥ)
  　＝２×矩形(ＡＦ)　
  　　　　　　【・・・(3)】

ところが
　ＡＦ、ＣＥの和は
　グノーモーンＩＪＫと
　正方形ＣＦとの
　和である。

• 公理１ー７（等しい）
  による。
• 　矩形(ＡＦ)＋矩形(ＣＥ)
  ＝グ(ＩＪＫ)＋矩形(ＣＦ)
  　　　　　　【・・・(4)】

したがって
　グノーモーンＩＪＫとＣＦとの和は
　ＡＦの２倍である。

• 公理１ー１（同じものに等しい）
  による。
• (3) (4) より、
  　２×矩形(ＡＦ)
  ＝グ(ＩＪＫ)＋矩形(ＣＦ)
  　 　　　　　　【・・・(5)】

ところが
　ＢＦはＢＣに等しいから、

• 命題２ー４の補足(正方形の対角線をはさむ正方形)
  による。

矩形ＡＢ、ＢＣの２倍も
　ＡＦの２倍である。

• 公理１ー５（同じものの２倍）
  による。
• 　２×矩形(ＡＦ)
  　＝２×矩形(ＡＢ、ＢＣ)
  　　　　　　【・・・(6)】

それゆえ
　グノーモーンＩＪＫと正方形ＣＦとの和は
　矩形ＡＢ、ＢＣの２倍に等しい。

• 公理１ー１（同じものに等しい）
  による。
• (5) (6) により
  　グ(ＩＪＫ)＋矩形(ＣＦ)
  　＝２×矩形(ＡＢ、ＢＣ)
  　　　　　　【・・・(7)】

双方に
　ＡＣ上の正方形であるＤＧが
　加えられたとせよ。

• 　矩形(ＤＧ)＝正方(_ＡＣ)
  　　　　　　【・・・(8)】

そうすれば
　グノーモーンＩＪＫと
　正方形ＢＧ、ＧＤとの
　和は
　ＡＢ、ＢＣにかこまれた矩形の２倍と
　ＡＣ上の正方形との
　和に等しい。

• 公理１ー２（等しいものに等しいものを加える）
  による。
• (7) (8) により
  　グ(ＩＪＫ)＋矩形(ＣＦ)＋矩形(ＧＤ)
  　＝２×矩形(ＡＢ、ＢＣ)＋矩形(ＧＤ)
  よって
  　グ(ＩＪＫ)＋矩形(ＢＧ)＋矩形(ＣＤ)
  　＝２×矩形(ＡＢ、ＢＣ)＋正方(_ＡＣ)
  　　　　　　【・・・(9)】

ところが
　グノーモーンＩＪＫと
　正方形ＢＧ、ＧＤとの
　和は
　ＡＤＥＢ全体とＣＦとの
　和に等しく、

• 公理１ー７（等しい）
  による。
• 　グ(ＩＪＫ)＋矩形(ＢＧ)BG＋矩形(ＧＤ)
  　＝矩形(ＡＤＥＢ)+矩形(ＣＦ)
  　　　　　　【・・・(10)】

これは
　ＡＢ、ＢＣ上の正方形の和である。

• (10) 、
  　矩形(ＡＤＥＢ)＋矩形(ＣＦ)
  　＝正方(_ＡＢ)＋正方(_ＢＣ)
  より
  　グ(ＩＪＫ)＋矩形(ＢＧ)＋矩形(ＤＧ)
  　＝正方(_ＡＢ)＋正方(_ＢＣ)
  【・・・(11)】

したがって
　ＡＢ、ＢＣ上の正方形の和は
　ＡＢ、ＢＣにかこまれた矩形の２倍と
　ＡＣ上の正方形と
　の和に等しい。

• 公理１ー１の補足（等しいものに等しい）
  による。
• (9) (11) より
  　２×矩形(ＡＢ、ＢＣ)＋正方(_ＡＣ)
  　＝正方(_ＡＢ)＋正方(_ＢＣ)
  

よってもし
　線分が
　任意に２分されるならば、
　全体の上の正方形と
　一つの部分の上の正方形と
　の和は
　全体の線分と
　この部分とにかこまれた矩形の２倍と
　残りの部分の上の正方形と
　の和に等しい。

これが証明すべきことであった。

• 以下の証明が可能である。
  　矩形ＡＢ、ＢＣは
  　命題２ー３（２分線分の全体と一つとによる矩形）
  により
  　矩形ＡＣ、ＢＣとＢＣ上の正方形と
  　の和に等しい。
  
  • 　矩形(ＡＢ、ＢＣ)＝矩形(ＡＣ、ＢＣ)＋正方(_ＢＣ)
    　　　　　　【・・・(12)】
  矩形ＡＢ、ＢＣの２倍は、
  　公理１ー５（同じものの２倍）
  により
  　矩形ＡＣ、ＢＣとＢＣ上の正方形と
  　の和の２倍に等しい。
  
  • (12) により
    　２×矩形(ＡＢ、ＢＣ)
    　＝２×（矩形(ＡＣ、ＢＣ)＋正方(_ＢＣ)）
    　　　　　　【・・・(13)】
  ２倍とは
  　２つ分のことであるから、
  　公理１ー１（同じものに等しい）
  により、
  　矩形ＡＣ、ＢＣとＢＣ上の正方形との和の２倍は
  　矩形ＡＣ、ＢＣの２倍とＢＣ上の正方形の２倍と
  　の和である。
  
  • 　２×（矩形(ＡＣ、ＢＣ)＋正方(_ＢＣ)）
    　＝２×矩形(ＡＣ、ＢＣ)＋２×正方(_ＢＣ)
    　　　　　　【・・・(14)】
  よって、
  　矩形ＡＢ、ＢＣの２倍は
  　公理１ー１（同じものに等しい）
  により
  　矩形ＡＣ、ＢＣの２倍とＢＣ上の正方形の２倍と
  　の和に等しい。
  
  • (13) (14) により
    　２×矩形(ＡＢ、ＢＣ)
    　＝２×矩形(ＡＣ、ＢＣ)＋２×正方(_ＢＣ)
    　　　　　　【・・・(15)】
  双方に
  　ＣＡ上の正方形を加えたとせよ。
  矩形ＡＢ、ＢＣの２倍とＣＡ上の正方形と
  　の和は
  　公理１ー２（等しいものに等しいものを加える）
  により、
  　矩形ＡＣ、ＢＣの２倍とＢＣ上の正方形の２倍とＣＡ上の正方形と
  　の和に等しい。
  
  • (15) により
    　２×矩形(ＡＢ、ＢＣ)＋正方(_ＣＡ)
    　＝２×矩形(ＡＣ、ＢＣ)
    　＋２×正方(_ＢＣ)＋正方(_ＣＡ)
    　　　　　　【・・・(16)】
  命題２ー４（２分線分上の正方形）
  により、
  　矩形ＡＣ、ＢＣの２倍とＢＣ上の正方形とＣＡ上の正方形と
  　の和は
  　ＡＢ上の正方形に等しい。
  
  • 　２×矩形(ＡＣ、ＢＣ)＋正方(_ＢＣ)＋正方(_ＣＡ)
    　＝正方(_ＡＢ)
    　　　　　　【・・・(17)】
  よって
  　矩形ＡＣ、ＢＣの２倍とＢＣ上の正方形の２倍とＣＡ上の正方形と
  　の和は
  　公理１ー２（等しいものに等しいものを加える）
  により、
  　ＡＢ上の正方形とＢＣ上の正方形と
  　の和に等しい。
  
  • (17) により
    　２矩形(ＡＣ、ＢＣ)＋２×正方(_ＢＣ)＋正方(_ＣＡ)
    　＝正方(_ＡＢ)＋正方(_ＢＣ)
    　　　　　　【・・・(18)】
  したがって
  　矩形ＡＢ、ＢＣの２倍とＣＡ上の正方形と
  　の和は
  　公理１ー１（同じものに等しい）
  により、
  　ＡＢ上の正方形とＢＣ上の正方形と
  　の和に等しい。
  • (16) (18) により
    　２矩形(ＡＢ、ＢＣ)＋正方(_ＣＡ)
    　＝正方(_ＡＢ)＋正方(_ＢＣ)
    
  • 命題2-7は第２巻の命題によると次のようになる。

    前提	作図	推論
    定義
    公準
    公理		1-1,1-2,1-5
    命題		2-3,2-4
    その他

• 本質的には差の平方のことである。
  　正方(_ＡＢ)＋正方(_ＢＣ)
  　＝２×矩形(ＡＢ、ＢＣ)
  　＋正方(_ＡＢーＢＣ)
  となり、
  　２×矩形(ＡＢ、ＢＣ)を移項すれ
  ば、
  　差ＡＢーＢＣの平方
  となる。
• 命題2-7は、
  　ＡＢ；線分
  に対して、
  　Ｃ；点（ＡＢ）
  をとるならば、
  　正方(_ＡＢ)＋正方(_ＢＣ)
  　＝２×矩形(ＡＢ、ＢＣ)＋正方(_ＣＡ)
  のことである。 　
• 命題2-7は推論用命題である。

  前提	作図	推論
  定義
  公準	1-1
  公理		1-1,1-1補,1-2,1-5,1-7
  命題	1-30補,1-31,1-43,1-46	2-4補
  その他

  　　

前 　　 次 　　 目次 　　頁頭