ユークリッド原論をどう読むか(16)
頁末
前
次
目次
ユークリッド原論
第11巻
命題11ー4(交わる2直線に垂直な直線はそれらを通る平面にも垂直)
(作図.交わる2直線の交点を通る、2直線に垂直な直線)
もし
一つの直線が
互いに交わる2直線に対し
それらの交点において
垂直に立てられた
ならば,
それらを通る
平面に対しても
垂直であろう。
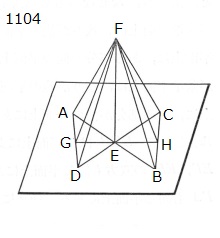
任意の線分EFが
点Eにおいて
互いに交わる
2線分AB,CDに対し
Eから垂直に立てられた
とせよ。
-
実際に
この垂線を
とることは、
この段階ではできない。
仮想的に、
とれたとして、
推論を進めている。
いわゆる、
幾何学的解析である。
この命題を用いた、
命題11ー4の補足(作図.交わる2直線の交点を通る、2直線に垂直な直線)
により、
実際に
この垂線を
とることができる。
-
EF⊥AB、
EF⊥CD
となっている。
EFは
AB,CDを通る平面に対しても
垂直である
と主張する。
AE,EB,CE,EDが
互いに等しく切りとられ,
Eを通り,
任意の線分GEHが
ひかれ,
AD,CBが
結ばれ,
さらに
任意の点Fから
FA,FG,FD,FC,FH,FBが
結ばれた
とせよ。
[......(1)]
-
命題1ー3の補足(作図.等しい線分となる点)
により、
B'(EB;EB'=EA)、
D'(ED;ED'=EC)、
をとり、
改めて、
それぞれをB、Dとしている。
-
AE=EB、
CE=ED
となっている。
そうすれば
2線分AE,EDは
2線分CE,EBに等しく,
等しい角をはさむ
-
前節、
命題1ー15(対頂角)
による。
-
AE=CE、
ED=EB、
∠AED=∠CEB
となっている。
から,
底辺ADは
底辺CBに等しく,
三角形AEDは
三角形CEBに等しいであろう。
[......(2)]
-
前節、
命題1ー4(2辺挟角相等)
による。
-
AD=CB、
△AED≡△CEB
となっている。
それゆえ
角DAEも
角EBCに等しい。
ところが
角AEGも
角BEHに等しい。
-
命題1ー15(対頂角)
による。
-
∠AEG=∠BEH
となっている。
ゆえに
AGE,BEHは
2角が
2角にそれぞれ等しく,
1辺が
1辺に,
すなわち
等しい2角にはさまれる辺AEが
EBに等しい
二つの三角形である。
-
前節、前々節、
(1)による。
-
∠AEG=∠BEH、
∠DAE=∠EBC
AE=BE
となっている。
したがって
残りの辺も
残りの辺に等しい
であろう。
-
前節、
命題1ー26(2角挟辺相等)
による。
-
EG=EH、
GA=HB、
∠EGA=∠EHB
となっている。
それゆえ
GEは
EHに,
AGは
BHに等しい。
[......(3)]
-
前節による。
-
GE=EH、
AG=HB、
となっている。
そして
AEは
EBに等しく,
FEは
共通でかつ垂直である
-
命題の設定、
(1)による。
-
AE=EB、
FE;共通、⊥AB
となっている。
から,
底辺FAは
底辺FBに等しい。
[......(4)]
-
前節、
命題1ー4(2辺挟角相等)
による。
-
FA=FB
となっている。
同じ理由で
FCも
FDに等しい。
-
前節、
(1)
による。
-
FC=FD
となっている。
そして
ADは
CBに等しく,
FAも
FBに等しい
-
(2)
による。
-
AD=CB、
FA=FB
となっている。
から,
2辺FA,ADは2辺 FB,BCにそれぞれ等しい。
そして
底辺FDが
底辺FCに等しい
ことは先に証明された。
-
前節、前々節
による。
-
FA=FB、
AD=BC、
FD=FC
となっている。
ゆえに
角FADも
角FBCに等しい。
-
前節、
命題1ー8(3辺相等2)
による。
-
∠FAD=∠FBC
となっている。
そしてまた
AGが
BHに等しい
ことは証明され,
他方FAは
FBに等しい
から,
2辺FA,AGは
2辺FB,BHに等しい。
そして
角FAGは
角FBHに等しい
ことが証明された。
-
前節、前々々節による。
-
FA=FB、
AG=BH、
∠FAG=∠FBH
となっている。
したがって
底辺FGは
底辺FHに等しい。
-
前節、
命題1ー4(2辺挟角相等)
による。
-
FG=FH
となっている。
そしてまた
GEは
EHに等しい
ことが証明され,
EFは
共通である
-
(3)
による。
-
GE=EH、
EF;共通
となっている。
から,
2辺GE,EFは
2辺HE,EFに等しい。
-
前節による。
-
GE=HE、
EF=EF
となっている。
そして
底辺FGは
底辺FHに等しい。
それゆえ
角GEFは
角HEFに等しい。
-
前節、前々節、
命題1ー8(3辺相等2)
による。
-
∠GEF=∠HEF
となっている。
ゆえに
角GEF,HEFの双方は
直角である。
-
前節、
命題1ー13(直線と2直角1)
による。
-
∠GEF=∠HEF=∠R
となっている。
したがって
FEは
Eを通って任意にひかれた
線分GHに対し垂直である。
-
∠AEDの間にEGがとられる場合について、
論証している。
-
FE⊥GH
となっている。
同様にして
FEは
それと会し,
かつ
基準平面上にある
すべての線分に対しても
垂直である
ことを証明しうる。
-
∠AECの間にEGがとられる場合についても、
同様である
ことを主張している。
-
EF⊥XY(基準平面;EF(交わる)EF)
となっている。
ところで
直線は
それと会し
かつ
一平面上にある
すベての直線に対し
垂直である
とき,
平面に対し垂直である。
それゆえ
FEは
基準平面に対し垂直である。
-
前節、前々節
による。
-
EF⊥基準平面
となっている。
ところが
基準平面は
線分AB,CDを通る平面である。
-
基準平面という表現は、
論証のかなり後半に出てくる。
意味的には、
今論じている平面ということである。
-
基準平面;平面(AB、CD;交点E(AB、CD))
となっている。
したがって
FEは
AB,CDを通る平面に対し垂直である。
-
前節、前々節
による。
-
FE⊥平面(AB、CD;交点E(AB、CD))
となっている。
よって
もし
一つの直線が
二つの互いに交わる
直線に対し
それらの交点において
垂直に立てられた
ならば,
それらを通る
平面に対しても
垂直であろう。
これが証明すべきことであった。
-
命題11ー2の補足(作図.交わる2直線、1直線上にない3点、1直線とその上にない1点で平面が決定)
により、
Eで交わる2直線AB、CDが
含まれている
基準平面
をとる。
公準1ー1の補足(作図.任意の点をとる)
により、
基準平面外の点Z
をとる。
命題11ー2の補足(作図.交わる2直線、1直線上にない3点、1直線とその上にない1点で平面が決定)
により、
ZとABが
含まれている
平面ZAB
をとる。
[......(5)]
命題1ー11(作図・線分からの垂線)
により、
Eを通る、
ABからの垂線
をとる。
公準1ー1の補足(作図.任意の点をとる)
により、
この垂線上に点Y
をとると、
AB⊥EY
となっている。
同様に
平面XABと点W
をとると、
AB⊥EW
となっている。
命題11ー2の補足(作図.交わる2直線、1直線上にない3点、1直線とその上にない1点で平面が決定)
により、
平面EWY
をとる。
命題11ー4(交わる2直線に垂直な直線はそれらを通る平面にも垂直)
ABは
Eを通る平面EWY上の直線と垂直
となる。
(5)以降の推論で、
直線ABをCDに
入れ替えると、
平面EUV
をとって、
CDが
Eを通る平面EUV上の直線と垂直
となる。
命題11ー3の補足2(作図.2平面の交線)
により、
平面EWYとEUVの交線EF
をとると、
EFは
AB、CDに対して垂直
となる。
よって、
交わる2直線の交点を通り、
2直線に垂直な直線
をとることができる。
(以下、命題11ー4の補足(作図.交わる2直線の交点を通る、2直線に垂直な直線)という。)
- 命題11ー4は、
交わる2直線に対し、
交点を通り、
2直線に垂直な直線は、
交点を通る
任意の直線に対し垂直
のことである。
交わる2直線に対し、
交点を通り、
2直線に垂直な直線は、
命題11ー4の補足により、
一方の直線を通る平面を2つとり、
交点からこの直線に垂直な直線を
それぞれの平面上でとり、
この2本の垂線を通る平面をとり、
交点からこの直線に垂直な直線
をとれば、
最初の2直線に垂直な直線となる。
-
命題11ー4の補足(作図.交わる2直線の交点を通る、2直線に垂直な直線)
- 命題11ー4は推論用命題である。
前
次
目次
頁頭
