ユークリッド原論をどう読むか(16)
頁末
前
次
目次
ユークリッド原論
第11巻
命題11ー5(交わる3直線に垂直な直線があれば、3直線は同一)
もし
直線が
相会する3直線に対し
それらの交点において
垂直に立てられた
ならば,
3直線は
一平面上にある。
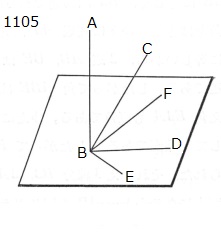
任意の線分ABが
3線分BC,BD,BEに対し
交点Bにおいて
垂直に立てられたとせよ。
-
実際的には、
命題11ー4の補足(作図.交わる2直線の交点を通る、2直線に垂直な直線)
により、
2直線に対して
垂直な直線をたてることができる。
3直線に対しては、
仮想的に
立てられた
として、
推論を進めている。
-
AB⊥BC、BD、BE
となっている。
BC,BD,BEは
一平面上にあると主張する。
そうでない
ならば,
もし
可能ならば,
BD,BEが
基準平面上にあり,
BCは
平面外にある
とし,
AB,BCを通る平面が
延長された
とせよ。
[......(H)]
-
背理法の仮定である。
命題11ー4の補足(作図.交わる2直線の交点を通る、2直線に垂直な直線)
により、
2本の直線に対しては、
常に立てることができる。
命題11ー2の補足(作図.交わる2直線、1直線上にない3点、1直線とその上にない1点で平面が決定)
により、
AB、BCを通る平面が
とれる。
-
BD、BE;基準平面上、
BD;基準平面外、
平面(AB、BC;)
となっている。
そうすれば
基準平面上に交線として線分をつくる
であろう。
BFをつくる
とせよ。
[......(1)]
-
2平面は、
共有点Bをもち、
一方は
ABを含まない
から、
互いに交わる面であり、
命題11ー3(2平面の交線は直線)
により、
交線BFをもつ。
なお、
点F(平面ABC;同じ側(C、AB))
とする。
[......(2)]
-
交線BF(平面ABC、基準平面;)
となっている。
そうすれば
3線分AB,BC,BFは
一平面上に,
すなわち
AB,BCを通って延長された
平面上にある。
-
(1)による。
-
AB、BC、BF;平面(AB、BC)上
となっている。
そして
ABは
BD,BEの双方に対し
垂直である
-
命題の設定である。
-
AB⊥BD、BE
となっている。
から,
ABは
BD,BEを通る平面に対しても
垂直である。
-
前節、
命題11ー4(交わる2直線に垂直な直線はそれらを通る平面にも垂直)
による。
-
AB⊥平面(BD、BE)
となっている。
ところが
BD,BEを通る平面は
基準平面である。
-
背理法の仮定による。
-
平面(BD、BE);基準平面
となっている。
ゆえに
ABは
基準平面に垂直である。
-
前節、前々節、
命題11ー4(交わる2直線に垂直な直線はそれらを通る平面にも垂直)
による。
-
AB⊥基準平面
となっている。
したがって
ABは
それと会し
かつ
基準平面上にあるすベての線分に対しても
直角をなすであろう。
-
前節、
定義11ー3(直角(直線・平面))
による。
-
AB⊥BZ(基準平面上;)
となっている。
ところが
BFは
基準平面上にあり
それと会する。
-
(1)
による。
-
BF;基準平面上
となっている。
それゆえ
角ABFは
直角である。
-
前節、前々節
による。
-
∠ABF=∠R
となっている。
ところが
角ABCも
直角である
ことが仮定されている。
-
命題の設定である。
-
∠ABC=∠R
となっている。
ゆえに
角ABFは
角ABCに等しい。
-
前節、前々節
による。
-
∠ABF=∠ABC=∠R
となっている。
そして
一平面上にある。
-
背理法の仮定による。
-
AB、CB、FB;面(AB、BC;)上
となっている。
これは不可能である。
-
(2)により、
C、Fは、
平面(AB、AC)上で、
ACについて、
同じ側にあり、
∠ABC=∠ABF
となり、
直線BCとBFは
一致し、
BC;基準平面上
となる。
これは、
背理法の仮定に反する。
したがって
線分BCは
平面外にない。
-
前節、背理法による。
-
BC;基準平面上
となっている。
ゆえに
3線分BC,BD,BEは
一平面上にある。
-
前節
による。
-
BC;平面(BD、BE)上
となっている。
よって
もし
一つの直線が
相会する3直線に対し
それらの交点において垂直に
立てられた
ならば,
3直線は
一平面上にある。
これが証明すべきことであった。
- 命題11ー5は、
交わる3直線BC、BD、BEに対して、
垂線BFが
たてられた
ならば、
3直線BC、BD、BEは、
同一平面上
のことである。
- 命題11ー5は推論用命題である。
前
次
目次
頁頭
