ユークリッド原論をどう読むか(16)
頁末
前
次
目次
ユークリッド原論
第11巻
命題11ー3(2平面の交線は直線)
交線
(作図.2平面の交線)
もし
2平面が
互いに交わる
ならば,
それらの交線は
直線である。
- 平面は、
定義1ー7による。
- 交わるは、
定義1ー14の補足による。
-
交線は、
面と面が
交わってできる
線をいう。
(以下、定義の補足(命題11ー3)
(交線)という。)
- 直線は、
定義1ー4による。
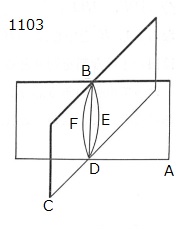
2平面AB,BCが
互いに交わる
とし,
線DBを
それらの交線
とせよ。
-
公準の補足2(命題11ー2)(作図.空間に任意の平面をとる)
により、
平面ABD
をとり、
平面BCD
をとる。
-
平面AB(交わる)平面BC、
BD;交線(AB、BC)
となっている。
線DBは
直線である
と主張する。
もし
そうでない
ならば,
DからBへ,平面AB上に
線分DEBが,
平面BC上に
線分DFBが
結ばれた
とせよ。
[......(1)]
-
背理法の仮定として、
点E(平面AB;¬平面BD)、
点F(平面BD;¬平面AB)
があって、
公準1ー1の補足2(作図.任意の線分)
により、
線分DEB(平面AB;¬平面BC)、
線分DFB(平面BC;¬平面AB)
をとる。
-
線分DEB(平面AB;¬平面BC)、
線分DFB(平面BC;¬平面AB)
となっている。
そうすれば
2線分DEB,DFBは
同じ端を
もち,
<明らかに面積を
かこむであろう。>
[D、Bは
平面AB上にある
から、
線分DFBは
平面AB上に
あであろう。]
-
線分DEB、DFBが
同一平面上にあれ
ば、
明らかである
が
同一平面上にある
と論証されていない。
証明の流れを尊重して、
修正している。
前節、
命題11ー1(平面上の直線は平面外に出ない)
による。
-
F;平面AB上
となっている。
これは不合理である。
それゆえ
DEB,DFBは
<直線ではない。>
[ともに、平面AB、BC上の線分で、一致し、
平面AB、BCの交線である。]
-
前節、
(1)、
背理法、
公理1ー9(2点を通る直線は一致)
による。
-
交線上の2点DBを通る
線分は一致し、
線分DEB、DFB;交線(平面AB、BC)
となっている。
同様にして
平面AB,BCの交線である
[直線]DB[上にない点は]<以外に
DからBへ結ばれる
他のいかなる直線も>
ありえない
ことを証明しうる。
-
背理法の仮定として、
交線上にあって、
直線DB上にない
点Gが
あった
とすれば、
公準1ー1(作図.直線)
により、
直線BG
をとると、
命題11ー1(平面上の直線は平面外に出ない)
により、
直線BGは、
交線上にあり、
(作図.交わる2直線、1直線上にない3点で平面が決定)
により、
交わる2直線BD、BGを含む平面
が定まり、
定義1ー6(面の端)
に矛盾するから
交線上の点は、
直線BD上にある。
-
直線BD以外の点は
交線上にない
となっている。
よって
もし
2平面が
互いに交わる
ならば,
それらの交線は
直線である。
-
前節、前々節による。
-
交線(2平面;);直線
となっている。
これが証明すべきことであった。
-
公準1ー1の補足(作図.任意の点をとる)
により、
交線上に2点
をとり、
公準1ー1(作図.直線)
により
2点を通る直線
をとれば、
命題11ー3(2平面の交線は直線)
により、
直線の交線が
とられる。
2平面を指定すれば、
直線の交線が与えられる。
(以下、命題11ー3の補足2
(作図.2平面の交線)という。)
- 命題11ー3は、
2平面が
交われば、
共通部分は
直線
のことである。
-
命題11ー3の補足2 (作図.2平面の交線)
- 命題11ー3は推論用命題である。
前
次
目次
頁頭
