ユークリッド原論をどう読むか（２）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー１５（対頂角）　
対頂角
もし
　２直線が互いに交わる
ならば、
　対頂角を互いに等しくする。

• 　直線は定義１ー４による。
• 　対頂角は、
  　２直線が互いに交わってできる４つの角のうち、
  　隣り合わない２つの角のことであり、
  　２組ある。
  （以下、定義の補足（命題１ー１５）という。）
• 　等しいは公理１ー７による。

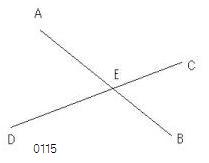
　２直線ＡＢ、ＣＤが
　点Ｅにおいて互いに交わる
とせよ。

• 　直線ＡＢ、ＣＤ、
  　交点Ｅ(ＡＢ,ＣＤ)
  をとっている。

　角ＡＥＣは角ＤＥＢに、
　角ＣＥＢは角ＡＥＤに等しい
と主張する。



　直線ＡＥは直線ＣＤの上に立ち、
　角ＣＥＡ、ＡＥＤをつくる
から、
　角ＣＥＡ、ＡＥＤの和は２直角に等しい。
　　　　　　【・・・(1)】

• 　命題１ー１３（直線と２直角１）
  による。
• 　∠ＣＥＡ＋∠ＡＥＤ＝２×∠Ｒ
  となっている。

また
　直線ＤＥは
　直線ＡＢの上に立ち
　角ＡＥＤ、ＤＥＢをつくる
から、
　角ＡＥＤ、ＤＥＢの和は２直角に等しい。

• 　命題１ー１３（直線と２直角１）
  による。
• 　∠ＡＥＤ＋∠ＤＥＢ＝２×∠Ｒ
  となっている。

そして
　角ＣＥＡ、ＡＥＤの和が
　２直角に等しい
ことも先に証明された。

• 　(1) による。
• 　∠ＣＥＡ＋∠ＡＥＤ＝２×∠Ｒ
  となっている。

それゆえ
　角ＣＥＡ、ＡＥＤの和は
　角ＡＥＤ、ＥＤＢの和に等しい。

• 　前節、前々節、
  　公理１ー１（同じものに等しい）
  による。
• 　∠ＣＥＡ＋∠ＡＥＤ
  　＝∠ＡＥＤ＋∠ＥＤＢ
  となっている。

　双方から角ＡＥＤが引き去られた
とせよ。

そうすれば
　残りの角ＣＥＡは残りの角ＢＥＤに等しい。

• 　公理１ー３（等しいものから等しいものをひく）
  による。
• 　∠ＣＥＡ＝∠ＢＥＤ
  となっている。

同様にして
　角ＣＥＢ、ＤＥＡが等しい
ことも証明されうる。

よってもし
　２直線が互いに交わる
ならば、
　対頂角を互いに等しくする。

　これが証明すべきことであった。

• 命題1-15は、
  　直線ＡＢ、ＣＤ、
  　交点Ｅ(ＡＢ,ＣＤ)
  をとるならば、
  　∠ＡＥＣ＝∠ＤＥＢ、
  　∠ＣＥＢ＝∠ＡＥＤ
  のことである。
  
• 命題1-15は推論用命題である。
  

  前提	作図	推論
  定義
  公準
  公理		1-1,1-3
  命題		1-13
  その他

前 　　 次 　　 目次 　　頁頭