ユークリッド原論をどう読むか(16)
頁末
前
次
目次
ユークリッド原論
第11巻
命題11ー2(交わる2直線、三角形は同一平面上)
(作図.交わる2直線、1直線上にない3点、1直線とその上にない1点で平面が決定)
(作図.空間に任意の平面をとる)
もし
2直線が
互いに交わる
ならば,
それらは
一平面上にあり,
そして
すベての三角形は
一平面上にある。
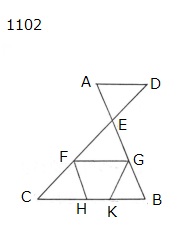
2線分AB,CDが
互いに点Eにおいて
交わるとせよ。
-
公準1ー1の補足(作図.任意の点をとる)
により、
点E、A、Cをとり、
公準1ー2(作図.直線の延長)
により、
AE、CEを延長し、
公準1ー1の補足(作図.任意の点をとる)
により、
B(延長AE)、
D(延長CE)
をとる。
-
B(延長AE)、
D(延長CE)
となっている。
AB,CDは
一平面上にあり,
また
すベての三角形は
一平面上にある
と主張する。
EC,EB上に
任意の点F,Gが
とられ,
CB,FGが
結ばれ,
FH,GKが
ひかれた
とせよ。
-
公準1ー1の補足(作図.任意の点をとる)
公準1ー1(作図.直線)
による。
-
F(EC;)、
G(EB;)、
CB(C、B;)、
FG(F、G;)、
H(BC;)、
K(BC;)、
FH(F、H)、
GK(G、K)
をとっている。
まず
三角形ECBは
一平面上にある
と主張する。
なぜなら
もし
三角形ECBの1部分FHCかGBKが
基準平面上に,
残りが
他の平面上にある
ならば,
[......(1)]
-
背理法の仮定である。
命題11ー1(平面上の直線は平面外に出ない)
により、
EC、EBの一方は、
基準平面上にある。
そこで、
ECが
基準平面上にある
とする。
命題の補足2(定義11ー18)(回転の軸上にない点は回転させると軸を含む平面上)
により、
三角形EBCの
辺CB上の点Kが
基準平面上にあるように
とると
命題11ー1(平面上の直線は平面外に出ない)
により、
CKも
ECとともに
基準平面上にある。
Hは
CK上にあるから、
命題11ー1(平面上の直線は平面外に出ない)
により、
FHも、三角FHCも
基準平面上にあるようにできる。
-
コメント(命題1ー4)(なぜならもし)
参照のこと。
-
三角FHC;基準平面上、
三角GBK;他の平面上
あるいは
その逆
となっている。
線分EC,EBの一方も,
ある部分が
基準平面上に,
ある部分が
他の平面上にあるであろう。
-
第2の背理法の仮定として、
両方が
基準平面上にあれば、
命題11ー1(平面上の直線は平面外に出ない)
により、
辺BCも
基準平面上にあり、
第1の背理法の仮定
(1)に反する
ことによる。
-
EC;基準平面上、
EB;基準平面外
あるいは、
その逆
となっている。
ところで
もし
三角形ECBの部分<FCBG>[FCH]が
基準平面上に,
<残り>[GBK]が
他の平面上にある
ならば,
-
本質的には、
場合分けの第一の場合;
基準平面上にあるのが三角形FCH
である。
もう一方の三角形GBKの場合も
推論は
まったく同じである
ので、
省略されている。
-
ここまでの流れ、
三角形FCHとGBKの一方が
基準平面上にあり、
他方が
基準平面上にない
と無関係な推論が進む。
可能な限り、
流れを尊重して、
原文を
修正する。
三角形FCHが
基準平面上にあるとしている。
-
三角FHC;基準平面上、
三角GBK;他の平面上
となっている。
<両>線分<EC,EB>[CB]も,
ある部分が
基準平面上に,
ある部分が
他の平面上にあるであろう。
-
前節による。
-
CH;基準平面上、
KB;基準平面外
となっている。
これは
不合理なることが
先に証明された。
-
前節、
命題11ー1(平面上の直線は平面外に出ない)
による。
それゆえ
三角形ECBは
一平面上にある。
[......(1)]
-
背理法による。
-
三角形ECB;基準平面上
となっている。
ところが
三角形ECBが
いかなる平面上にあろうと,
EC,EBの双方も
同じ平面上にあり,
-
前節による。
-
EC、EB;同一平面上
となっている。
EC,EBの双方が
いかなる平面上にあろうと,
AB,CDも
同じ平面上にある。
-
前節、
命題の設定
命題11ー1(平面上の直線は平面外に出ない)
による。
-
AB、CD;EC、CBと同一平面上
となっている。
ゆえに
線分AB,CDは
一平面上にあり,
そして
すベての三角形は
一平面上にある。
-
前節、
(1)
による。
-
AB、CD;同一平面上、
任意の三角形;同一平面上
となっている。
これが証明すべきことであった。
-
公準1ー1の補足(作図.任意の点をとる)
により、
異なる2点A、Bを
とり、
公準1ー1(作図.直線)
により、
直線ABを
引く。
公準1ー1の補足(作図.任意の点をとる)
により、
点Z(¬AB;)
をとり、
公準1ー1(作図.直線)
により、
直線AZ
を引く。
AB、AZは
交わる2直線
だから、
命題11ー2(交わる2直線、三角形は同一平面上)
により、
AB、AZは
同一平面上
にある。
交わる2直線を含む平面は
唯一である。
背理法の仮定として、
2つある
としたら
一方の平面上にあって、
他方の平面上にない
点Yがあり、
AB、AZ上にはない。
Yを乗せる平面上で、
命題1ー31(作図・平行線)
により、
Yを通りABに平行な直線YXを引く。
命題1ー30の補足(交線に平行な線)
により、
YXは、
AZと交わり、
交点をW
とする。
公準1ー1の補足(作図.任意の点をとる)
により、
AZ上で、Wと異なる点V
をとる。
命題1ー31の補足(与点を通る平行線は唯一)
により、
YVは、
ABに平行でない
から、
定義1ー23(平行(線))
により、
ABと交わり、
交点をUとする。
U、Vは
AB、AZ上の点
だから、
どちらの平面にも含まれる。
命題11ー1(平面上の直線は平面外に出ない)
により、
Yも
どちらの平面にも含まれる。
背理法の仮定に矛盾するから、
交わる2直線を含む平面は
唯一である。
よって、
交わる2直線が
平面を決める。
したがって、
1直線上にない3点、
1直線とその上にない1点が
平面を決める。
(以下、命題11ー2の補足(作図.交わる2直線、1直線上にない3点、1直線とその上にない1点で平面が決定)という。)
-
公準1ー1の補足(作図.任意の点をとる)
により、
空間に任意の2点をとり、
公準1ー1(作図.直線)
により、
2点を結び、
公準1ー1の補足(作図.任意の点をとる)
により、
直線外に任意の1点をとり、
命題11ー2の補足(作図.交わる2直線、1直線上にない3点、1直線とその上にない1点で平面が決定)
により、
平面を決めることができる。
よって、
空間に任意の直線をとることができる。
(以下、公準の補足2(命題11ー2)
(作図.空間に任意の平面をとる)という。)
- 命題11ー2は、
2直線AB、CDが
交われ
ば、
同一平面上、
三角形は、
同一平面上
のことである。
-
公準の補足2(命題11ー2) (作図.空間に任意の平面をとる)
-
命題11ー2の補足(作図.交わる2直線、1直線上にない3点、1直線とその上にない1点で平面が決定)
- 命題11ー2は推論用命題である。
前
次
目次
頁頭
