ユークリッド原論をどう読むか(3)
頁末
前
次
目次
ユークリッド原論
第1巻
命題1ー26(2角挟辺相等)
(2角挟辺相等による合同)
もし二つの三角形において
2角が2角にそれぞれ等しく、
1辺が1辺に、
すなわち
等しい2角にはさまれる辺か
または
等しい角の一つに対する辺が等しければ、
残りの2辺も残りの2辺に等しく、
残りの角も残りの角に等しいであろう。
ABC、DEFを
2角ABC、BCAが2角DEF、EFDに等しい、
すなわち
角ABCが角DEFに、
角BCAが角EFDにそれぞれ等しい
二つの三角形とせよ。
そして1辺が1辺に、
まず
等しい角にはさまれる辺
すなわちBCがEFに
等しいとせよ。
残りの2辺もそれぞれ残りの2辺に、
すなわち
ABはDEに、
ACはDFに等しく、
また
残りの角も残りの角に、
すなわち
角BACは角EDFに
等しいと主張する。
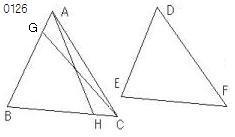
もしABがDEに等しくなければ、
それらの一方は大きい。
ABを大きいとし、
BGがDEに等しくされ、
【・・・(a)】
- DEが大きければ、
以下の論証を同様に行えばよい。
- 命題1ー3(作図・等しい線分を切り取る)
による。
-
AB>DE
BG=DE
としている。
GCが結ばれたとせよ。
そうすれば
BGはDEに等しく、
BCはEFに等しいから、
2辺BG、BCは
2辺DE、EFにそれぞれ等しい。
そして
角GBCは角DEFに等しい。
-
∠GBC=∠ABC
であり、
命題の設定
による。
-
(BG,BC)=(DE,EF)、
∠GBC=∠DEF
となっている。
それゆえ
底辺GCは底辺DFに等しく、
三角形GBCは三角形DEFに等しく、
残りの角は残りの角に等しい、
すなわち
等しい辺が対する角は等しい
であろう。
- 命題1ー4(2辺挟角相等)
である。
-
GC=DF、
△GBC≡△DEF
となっている。
ゆえに
角GCBは角DFEに等しい。
ところが
角DFEは角BCAに等しいと仮定されている。
- 命題の設定
による。
-
∠DFE=∠BCA
となっている。
したがって角BCGは角BCAに等しく、
- 公理1ー1(同じものに等しい)
による。
-
∠BCG=∠BCA
となっている。
小さいものが大きいものに等しい。
これは不可能である。
-
(a)により、
∠BCG<∠BCA
となっている。
それゆえ
ABはDEに不等でない。
ゆえに等しい。
しかも
BCはEFに等しい。
よって
2辺AB、BCは
2辺DE、EFにそれぞれ等しい。
しかも
角ABCは角DEFに等しい。
-
前節、前々節、命題の設定
による。
-
(AB,BC)=(DE,EF)、
∠ABC=∠DEF
となっている。
したがって
底辺ACは底辺DFに等しく、
残りの角BACは残りの角EDFに等しい。
さてまた
等しい角に対する辺、
たとえば
ABがDE
に等しいとせよ。
このときも
残りの辺は残りの辺に、
すなわち
ACはDFに、
BCはEFに等しく、
また
残りの角BACは残りの角EDFに
等しいと主張する。
- 2角にはさまれる辺以外の辺が
等しい場合を検討する。
もし
BCがEFに不等であれば、
それらの一方は大きい。
もし可能ならば、
- 背理法の仮定である。
- 「もし可能ならば」は、
コメント2(命題1−7)参照のこと。
なお、
本命題の前半の論証における
背理法においては、
この一言がない。
BCが大きいとし、
BHがEFに等しくされ、
- 命題1ー3(作図・等しい線分を切り取る)
による。
AHが結ばれたとせよ。
【・・・(b)】
BHはEFに、
ABはDEに等しいから、
2辺AB、BHは
2辺DE、EFにそれぞれ等しい。
そして
等しい角をはさむ。
-
前節、前々節、
命題の設定
による。
-
(AB,BH)=(DE,EF)、
∠ABH(ABC)=∠DEF
のことである。
それゆえ
底辺AHは底辺DFに等しく、
三角形ABHは三角形DEFに等しく、
残りの角は残りの角に、
すなわち
等しい辺が対する角は
等しいであろう。
- 命題1ー4(2辺挟角相等)
のことである。
-
AH=DF、
△ABH≡△DEF
となっている。
ゆえに
角BHAは角EFDに等しい。
ところが
角EFDは角BCAに等しい。
- 命題の設定
による。
-
∠EFD=∠BCA
となっている。
かくて
三角形AHCの外角BHAは
内対角BCAに等しい。
-
前節、前々節、
公理1ー1(同じものに等しい)
による。
-
∠BHA=∠BCA
となっている。
これは不可能である。
それゆえ
BCはEFに不等でない。
ゆえに等しい。
しかもABはDEに等しい。
このとき
2辺AB、BCは2辺DE、EFに
それぞれ等しい。
そして
等しい角をはさむ。
-
前節、前々節、命題の設定
による。
-
(AB,BC)=(DE,EF)、
∠ABC=∠DEF
となっている。
したがって
底辺ACは底辺DFに等しく、
三角形ABCは三角形DEFに等しく、
残りの角BACは残りの角EDFに等しい。
- 命題1ー4(2辺挟角相等)
による。
-
AC=DF、
△ABC≡△DEF
となっている。
よって
[
2つの場合より
]
もし
二つの三角形において
二つの角が二つの角にそれぞれ等しく、
1辺が1辺に、
すなわち
等しい2角にはさまれる辺か
または
等しい角の一つに対する辺が
等しければ、
残りの2辺も残りの2辺に等しく、
残りの角も残りの角に等しいであろう。
これが証明すべきことであった。
- 前半は
いわゆる二角挟辺相等の合同条件である。
命題1ー4(2辺挟角相等)、
命題1ー8(3辺相等2)
と異なって、
動かして重ね合わせる論法ではない。
- 後半では、
三角形の内角の和が
2直角である(命題1ー32)ということを
前提としていないことに注目したい。
この段階では前半に帰着させることが
できないのである。
- 前半、後半いずれにおいても、
命題1ー4(2辺挟角相等)
により
残りの2辺と
残りの角が
等しいことを論証している。
したがって
2つの三角形が等しい
ことも論証されていることになる。
すなわち、
2つの三角形において、
対応する2角と1辺が等しければ、
残りの1角と2辺がそれぞれ等しく、
2つの三角形は等しい。
(以下、命題1ー26の補足(2角挟辺相等による合同)という。)
しかし、
ここで
2つの三角形が等しい
ことが明記されていないため、
命題1ー34(平行四辺形の対辺・対角・対角線)
で
推論がもたもたすることになる。
-
命題1-26、命題1-26の補足は、
∠ABC=∠DEF、
∠BCA=∠EFD
となる
△ABC、△DEF
に対して、
BC=EF
または、
AB=DE
または
AC=DF
ならば、
△ABC≡△DEF
のことである。
-
命題1ー26の補足(2角挟辺相等による合同)
| 前提 | 作図 | 推論 |
| 定義 |
|
|
| 公準 |
|
|
| 公理 |
|
|
| 命題 |
|
1-26
|
| その他 |
|
|
-
1ー26は推論用命題である。
前
次
目次
頁頭
