ユークリッド原論をどう読むか(14)
頁末
前
次
目次
ユークリッド原論
第10巻
命題10ー14助(作図.線分上の正方形の差となる正方形の辺)
(作図.2線分の正方形の和となる正方形)
(作図.線分上に半円)
補 助 定 理
2つの不等な線分が与えられた
とき、
大きい線分上の正方形が
小さい線分上の正方形より
いかなる正方形だけ大きいか
《を見いだすこと。》
[その辺となる線分をつくること。]
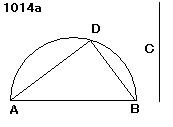
与えられた不等な2線分をAB、C
とし、
そのうち
ABが大きい
とせよ。
-
公準1ー1の補足2(作図.任意の線分)
により、
任意の線分ABをとり、
公準1ー1の補足(作図.任意の点をとる)
により
AB上に点C'をとり、
命題1ー2(作図・線分)
により
任意の位置に
AC'に等しい線分Cをとる。
-
AB>C
となっている。
このとき
AB上の正方形は
C上の正方形より
いかなる正方形だけ大きいか
を見いださねばならぬ。
AB上に半円ADBが描かれた
とし、
-
命題1ー10(作図・線分の2等分)
により
AB上に中点Eをとり、
公準1ー3(作図.円)
により
中心E、半径EAの円をかく。
直径ABで区切られた
一方の円周と直径ABによる図形が
求める半円である。
よって、
与えられた線分を直径
として、
半円をとる
ことができる。
(以下、命題10ー14補助の補足2
(作図.線分上に半円)という。)
それにCに等しいADが挿入され、
[......(a)]
DBが結ばれた
とせよ。
そうすれば
角ADBが直角であること、
-
(a)、
命題3ー31(半円内の角は直角、半円より大小の切片内の角、切片の角)
による。
-
角ADB=直角
となっている。
AB上の正方形が
AD、すなわち
C上の正方形より、
DB上の正方形だけ大きい
ことは明らかである。
-
(a)、
命題1−47(三平方の定理)
による。
-
sq(_AB)=sq(_C)+sq(_DB)
となっている。
同様にして
2線分が与えられた
とき、
それらの上の正方形の和に
等しい正方形の辺
《もこのようにして見いだされる。》
[となる線分をつくること。]
(以下、命題10ー14助の系
(作図.2線分の正方形の和となる正方形の辺)という。)
与えられた2線分をAD、DB
とし、
それらの上の正方形の和に
等しい正方形の辺
を見いださねばならぬとせよ。
それらの2線分が定められ、
直角AD、DBをかこむ
[......(b)]
-
命題1ー11(作図・線分からの垂線)
により、
AD上のDから垂線をひき、
命題1ー3の補足(作図.等しい線分となる点)という。)
により
DBに等しくなるように
DB’をとる。
B’を改めてB
とし、
Bを溯ってもちいている。
とし、
ABが結ばれた
とせよ。
AD、 DB上の正方形の和に
等しい正方形の辺がAB
であることは明らかである。
-
(b)、
命題1−47(三平方の定理)
による。
-
sq(_AD)+sq(_DB)=sq(_AB)
となっている。
これが証明すべきことであった。
-
この補助定理が
命題10−14
のためにある
ことは明白である。
命題10−14
を見ると、
論証のため
ではなく、
命題の設定となる図を作るために
補助定理を必要としている。
このことから、
原論は
命題の設定に関して
具体的作図を重視している
と見ることができる。
-
命題10ー14助は、
2線分A、B;A>B、
に対し、
線分C;A斜辺、B、C直角を挟む直角三角形
をとると、
sq(_C)=sq(_A)ーsq(_B)。
命題10ー14助の系は、
2線分A、B
に対し、
線分C;A、Bが直角を挟む
直角三角形の斜辺
をとると、
sq(_C)=sq(_A)+sq(_B)。
のことである。
-
命題10ー14助の系 (作図.2線分の正方形の和となる正方形の辺)
-
命題10ー14補助の補足2 (作図.線分上に半円)
- 命題10ー14助は作図用命題である。
前
次
目次
頁頭
