ユークリッド原論をどう読むか（２）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー１８（三角形の大きい辺と大きい角１）
　すべての三角形において
　大きい辺は
　大きい角に対する。

• 　三角形は定義１ー１９の補足２による。
• 　大きいは公理１ー８による。
• 　辺は定義１ー１９の補足による。
• 　角は定義１ー８による。

　ＡＢＣを
　辺ＡＣがＡＢより大きい
　三角形
とせよ。

• 　△ＡＢＣ(;;ＡＣ＞ＡＢ)
  をとっている。

　角ＡＢＣも
　角ＢＣＡより大きい
と主張する。


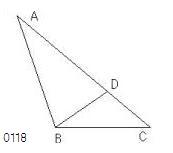
　ＡＣはＡＢより大きい
から、
　ＡＤがＡＢに等しくされ、

• 　命題１ー３（作図・等しい線分を切り取る）
  による。
• 　点Ｄ(ＡＣ;;ＡＤ＝ＡＢ)
  をとっている。

　ＢＤが結ばれた
とせよ。
　　　　　　【・・・(a)】

• 　公準１ー１（作図.直線）
  による。
• 　線分(Ｂ,Ｄ)
  をとっている。

そうすれば
　角ＡＤＢが
　三角形ＢＣＤの外角である
から、
　内対角ＤＣＢより大きい。
　　　　　　【・・・(1)】

• 　命題１ー１６（外角と内対角）
  による。
• 　∠ＡＤＢ＞∠ＤＣＢ
  となっている。

ところが
　辺ＡＢは辺ＡＤに等しい
から、
　角ＡＤＢは角ＡＢＤに等しい。

• 　命題１ー５（２等辺三角形の底角）
  による。
• 　∠ＡＤＢ＝∠ＡＢＤ
  となっている。

ゆえに
　角ＡＢＤも角ＡＣＢより大きい。

• 　(1) ,
  　公理１ー８の補足２（等より大・小、大・小に等）
  による。
• 　∠ＡＢＤ＞∠ＡＣＢ
  となっている。

それゆえなおさら
　角ＡＢＣは角ＡＣＢより大きい。

• 　(a) ,
  　公理１ー８の補足３（大きい・小さいものより大きい・小さい）
  による。

よって
　すべての三角形において
　大きい辺は
　大きい角に対する。
　
　これが証明すべきことであった。

• 命題1-18は、
  　△ＡＢＣ
  において、
  　ＡＣ＞ＡＢ
  ならば
  　∠ＡＢＣ＞∠ＢＣＡ
  ということである。
• 命題1-18は推論用命題である。

  前提	作図	推論
  定義
  公準	1-1
  公理		1-8補2,1-8補3
  命題	1-3	1-5、1-16
  その他

前 　　 次 　　 目次 　　頁頭