ユークリッド原論をどう読むか（１４）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第１０巻
　
命題１０ー１３（通約量と非通約なら非通約）

もし
　２つの量が通約でき、
　それらの一方が
　何らかの量と通約できない
ならば、
　残りも同じ量と通約できない
であろう。

• 量は、
  定義５ー１の補足による。
• 通約は、
  定義１０ー１による。

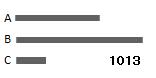
　Ａ、Ｂを２つの通約できる量
とし、
　それらの一方Ａが
　他の何らかの量Ｃと通約できない
とせよ。

• 　「量（について）・・・とせよ」は、
  　コメント６（命題５ー１）
  　参照のこと。
  
• 　量を線分で表現する
  とすれば、
  　作図は次のようになる。
  
  　公準１ー１の補足２（作図.任意の線分）
  により
  　任意の線分Ａをとる
  　命題１０ー６の系３（作図.長さ・平方で通約可の線分)
  により
  　Ａと通約できる線分Ｂをとる。
  　命題１０ー１０（作図.長さ・平方において通約でない線分）
  により
  　Ａと通約できない線分Ｃをとる。
• 　Ａ∩Ｂ、Ａ¬∩Ｃ
  となっている。

　残りのＢもＣと通約できない
と主張する。

もし
　ＢがＣと通約でき、

• 　背理法の仮定をのべている。
• 　Ｂ∩Ｃ
  としている。

　他方ＡがＢと通約できる

• 　命題の設定による。
• 　Ａ∩Ｂ
  となっている。

ならば、
　ＡとＣも通約できる。

• 　前節、前々節、
  　命題１０ー１２（同じ量と通約なら通約）
  による。
• 　Ａ∩Ｃ
  となっている。

ところが
　通約できなくもある。

• 　命題の設定による。
• 　Ａ¬∩Ｃ
  となっている。

　これは不可能である。

したがって
　ＢはＣと通約できる
のではない。

• 　背理法による。
• 　Ｂ¬∩Ｃ
  となる。

ゆえに
　通約できない。

• 　Ｂ¬∩Ｃ
  のことである。
  

よって
もし
　２つの量が通約でき云々

• 　云々は 「それらの一方が
  　何らかの量と通約できない
  ならば、
  　残りも同じ量と通約できない
  であろう。
  

• 命題１０ー１３は、
  　Ａ∩ＢでＡ¬∩Ｃ
  ならば、
  　Ｂ¬∩Ｃ
  のことである。
• 命題１０ー１３は推論用命題である。

  前提	作図・構成	推論
  定義
  公準	1-1補2
  公理
  命題	10-6系3,10-10	10-12
  その他	コ6(題5-1)

前 　　 次 　　 目次 　　頁頭