ユークリッド原論をどう読むか（２）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー１０（作図・線分の２等分）
中点
　与えられた線分を２等分する
こと。

• 　線分は定義１ー４の補足による。
• 　２等分は定義の補足（公理１ー６）による。

　与えられた線分をＡＢ
とせよ。

• 　線分(Ａ,Ｂ)
  をとっている。

このとき
　線分ＡＢを
　２等分しなければならぬ。

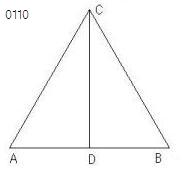
　その上に等辺三角形ＡＢＣがつくられ、

• 　命題１ー１（作図・正三角形）
  による。
• 　Ｃ;点(△ＡＢＣ≡正三(_ＡＢ))
  をとっている。

　角ＡＣＢが
　線分によって２等分された
とせよ。
　　　　　　【・・・(a)】

• 　命題１ー９（作図・角の２等分）
  による。
• 　角ＡＣＢを２等分した半直線ＣＥと
  　ＡＢとは交点Ｄをもつ。
  なぜなら、
  　半直線ＣＥは、
  　等辺三角形ＡＢＣのＣから内部を通って
  　無限に伸びている
  ので、
  　辺ＡＢについて
  　反対側の２点を通っており、
  　命題の補足３（定義１ー１４）
  　により
  　ＣＥとＡＢは交点をもつ。
  　それをＤ
  とする。
• 　Ｄ;点(ＡＢ,∠ＡＣＤ＝∠ＢＣＤ)
  をとっている。

［そうすると、］
　線分ＡＢは
　点Ｄにおいて
　２等分されている
と主張する。

　ＡＣはＣＢに等しく、

• 　(a) により
  　ＡＢＣは等辺三角形である
  ことによる。
• 　ＡＣ＝ＣＢ
  となっている。

　ＣＤは共通である
から、
　２辺ＡＣ、ＣＤは
　２辺ＢＣ、ＣＤに
　それぞれ等しい。
そして、
　角ＡＣＤは角ＢＣＤに等しい。

• 　前節、
  　(a) により、
  　ＣＤは角ＡＣＢの２等分線となる
  ことによる。
• 　(ＡＣ,ＣＤ)＝(ＢＣ,ＣＤ)、
  　∠ＡＣＤ＝∠ＢＣＤ
  となっている。

ゆえに
　底辺ＡＤは底辺ＢＤに等しい。

• 　前節、
  　命題１ー４（２辺挟角相等）
  による。
• 　ＡＤ＝ＢＤ
  となっている。

よって
　与えられた線分ＡＢは
　点Ｄにおいて２等分されている。
　これが作図すべきものであった。

• 　線分を２等分する点のことを
  　中点 という。
  (以下、定義の補足（命題１ー１０） 中点という。)
  
• 命題1-10は、
  　ＡＢ；線分
  に対して、
  　Ｃ；頂点.正三(_ＡＢ)、
  　Ｄ；交点(ＡＢ,２等分線(∠ＡＣＢ)）
  をとるならば、
  　Ｄ；中点.ＡＢ
  のことである。
  
• 命題1-10は作図用命題である。
  

  前提	作図	推論
  定義
  公準
  公理
  命題	補3(義1-14)、1-1、1-9	1-4
  その他

前 　　 次 　　 目次 　　頁頭