ユークリッド原論をどう読むか（１２）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第８巻
　
命題８ー３（最小順次比例数の外項は互に素）
もし
　順次に比例する任意個の数が
　それらと同じ比をもつ数のうち
　最小である
ならば、
　それらの外項は
　互いに素である。

• 順次に比例は、 定義の補足（命題８ー１）による。
• 数は、 定義７ー２による。
• 同じ比は、 定義５ー５による。
• 最小は、 定義の補足３（命題３ー７）による。
• 外項は、 定義の補足（命題６ー１６）による。
• 互いに素は、 定義７ー１３による。

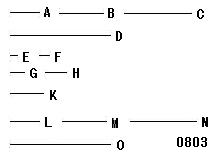
　Ａ、Ｂ、Ｃ、[…、Ｃ_k、…、]Ｄを
　それらと同じ比をもつ数のうち
　最小である、
　任意個の順次に比例する数
とせよ。

• 準一般的な証明である。
  コメント２（命題５ー１） 参照のこと。
  
• 「数（について）・・・とせよ」は、
  コメント４（命題７ー１） 参照のこと。
• Ａ：Ｂ＝…＝Ｃ_k：Ｃ_k+1＝…＝Ｃ_n-2：Ｄ(最小ｎ項)
  となっている。
  

　それらの外項Ａ、Ｄは
　互いに素である
と主張する。

　Ａ、Ｂ、Ｃ、[…、Ｃ_k、…、]Ｄの比をなす数のうちで
　最小である二つの数Ｅ、Ｆが、
　　　　　　[......(ａ)]

• 命題７ー３３（任意個の比例で最小数）
  による。
• Ｃ₁＝Ａ、Ｃ₂＝Ｂ、Ｃ₃＝Ｃ、Ｃ_n＝Ｄ
  とする。
• Ａ：Ｂ＝Ｅ：Ｆ(最小)
  となっている。
  

　ついで
　三つの数Ｇ、Ｈ、Ｋがとられ、
　　　　　　[......(ｂ)]

• Ｅ、Ｆから 命題８ー２（順次に比例する数）
  による。
• Ａ：Ｂ＝Ｅ：Ｆ(最小)。
  Ｅ×Ｅ＝Ｇ、Ｅ×Ｆ＝Ｈ、
  Ｆ×Ｆ＝Ｋ
  となっている。
  

　そして
　次々に一つずつ多くして、
　とられた数が
　Ａ、Ｂ、Ｃ、[…、Ｃ_k、…、]Ｄと同じ個数になるようにせよ。

• Ｅ、Ｆから 命題８ー２（順次に比例する数） による。
• 　Ｅ^n-1、Ｅ^n-2Ｆ、Ｅ^n-3Ｆ²、Ｅ^n-kＦ^k-1、Ｆ^n-1
  となっている。

　かかる数がとられた
とし、
　それらをＬ、Ｍ、Ｎ、[…、Ｎ_k、…、]Ｏ
とせよ。
[......(Ｃ)]

• Ａ：Ｂ＝Ｅ：Ｆ(最小)。
  　Ｌ＝Ｅ^n-1、Ｍ＝Ｅ^n-2Ｆ、Ｎ＝Ｅ^n-3Ｆ²、Ｎ^k＝Ｅ^n-kＦ^k-1、Ｏ＝Ｆ^n-1
  となっている。
  Ａ、Ｂ、Ｃ、[…、Ｃ_k、…、]ＤとＬ、Ｍ、Ｎ、[…、Ｎ_k、…、]Ｏは個数も同じ。

そうすれば
　Ｅ、Ｆは
　それらと同じ比をもつ数のうち
　最小である

• （ａ）による。
• Ａ：Ｂ＝Ｅ：Ｆ(最小)
  となっている。

から、
　互いに素である。

• 命題７ー２２（同じ比の最小の２数は互いに素） による。
• 　Ｅ;(互いに素)Ｆ
  となっている。

そして
　Ｅ、Ｆは
　２乗してそれぞれＧ、Ｋをつくり、
　Ｇ、ＫにかけてそれぞれＬ、Ｏをつくった

• （ｂ）、 （ｃ） による。
• 　Ｅ²＝Ｇ、Ｆ²＝Ｋ、
  　Ｅ×Ｅ^n-2＝Ｌ^n-1、Ｆ×Ｋ^n-2＝Ｏ^n-1
  となっている。

から、
　ＧはＫと、
　ＬはＯと互いに素である。
　　　　　　[......(１)]

• 命題７ー２６（２数が２数に対して素の積）
  による。

そして
　Ａ、Ｂ、Ｃ、[…、Ｃ_k、…、]Ｄは
　それらと同じ比をもつ数のうち
　最小であり、

• 命題の設定による。
• 　Ａ：Ｂ＝…＝Ｃ_k：Ｃ_k+1＝…＝Ｃ_n-2：Ｄ(最小)

　Ｌ、Ｍ、Ｎ、[…、Ｎ_k、…、]Ｏは
　Ａ、Ｂ、Ｃ、[…、Ｃ_k、…、]Ｄと同じ比をなす数のうちで
　最小であり、

• 命題８ー２（順次に比例する数） による。

　Ａ、Ｂ、Ｃ、[…、Ｃ_k、…、]Ｄの個数は
　Ｌ、Ｍ、Ｎ、[…、Ｎ_k、…、]Ｏの個数に等しい
から、

• （ｃ）による。

　Ａ、Ｂ、Ｃ、[…、Ｃ_k、…、]Ｄのおのおのは
　Ｌ、Ｍ、Ｎ、[…、Ｎ_k、…、]Ｏのおのおのに等しい。

• 　Ａ＜＝Ｌ、Ｌ＜＝Ａである
  から
  　Ａ＝Ｌとなる。
  （ｃ）により、
  　Ａ：Ｂ＝Ｌ：Ｍとなり、
  　Ａ＝Ｌである
  から
  　命題５ー９（同一比の量）により
  　Ｂ＝Ｍとなる。
  以下同様に、
  Ｃ＝Ｎ、Ｄ＝Ｏとなる。
  
• 　Ａ＝Ｌ、Ｂ＝Ｍ、Ｃ_k＝Ｎ_k、Ｄ＝Ｏ
  となっている。

それゆえ
　ＡはＬに、
　ＤはＯに等しい。

そして
　Ｌ、Ｏは
　互いに素である。

• （１）による。
• 　Ｌ;(互いに素)Ｏ
  となっている。

したがって
　Ａ､Ｄも互いに素である。

• 前節、前々節による。
• 　Ａ;(互いに素)Ｄ
  となっている。

　これが証明すべきことであった。

• 命題８ー３は、
  　Ａ：Ｂ＝…＝Ｃ_k：Ｃ_k+1＝…＝Ｃ_n-2：Ｄ(最小ｎ項)
  ならば、
  　Ａ;(互いに素)Ｄ
  のことである。
• 命題８ー３は推論用命題である。

  前提	作図	推論
  定義
  公準
  公理
  命題	7-33	5-9,7-22,7-26,8-2
  その他	コ4(題7-1)

前 　　 次 　　 目次 　　頁頭