ユークリッド原論をどう読むか（１１）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第７巻
　
命題７ー２６（２数が２数に対して素の積）
もし
　２つの数が
　共に別の２つの数の双方に対し素である
ならば、
　それらの積も
　互いに素
であろう。

• 数は、 定義７ー２による。
• 対し素は、 定義の補足（命題７ー２３）による。
• 積は、 定義７ー１６の補足２による。
• 互いに素は、 定義７ー１３による。

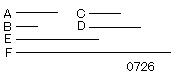
　２数Ａ、Ｂが
　ともに２数Ｃ、Ｄの双方に対し素である
とし、

• 「数（について）・・・とせよ」は、
  コメント４（命題７ー１） 参照のこと。
• 　「互いに素な３個以上の数」は、
  　コメント(命題７ー２４）
  　参照のこと。
  現段階では仮想的である。
• 　任意の数Ａ、Ｂ
  に対し、
  　数Ｃ[;;(互いに素)(Ａ、Ｂ)]、
  　数Ｄ[;;(互いに素)(Ａ、Ｂ)]
  をとっている。
  　Ａ;¬(互いに素)Ｂ
  　Ｃ;¬(互いに素)Ｄ
  となっていても構わない。

　ＡがＢにかけてＥをつくり、
　ＣがＤにかけてＦをつくる
とせよ。

• 定義７ー１６（かけるの定義）
  による。
• 　数Ｅ(;;＝Ａ×Ｂ)、
  　数Ｆ(;;＝Ｃ×Ｄ)
  をとっている。

　Ｅ、Ｆは互いに素である
と主張する。

　Ａ、Ｂの双方は
　Ｃに対し素である

• 命題の設定による。
• 　(Ａ、Ｂ);(互いに素)Ｃ
  となっている。

から、
　Ａ、Ｂの積も
　Ｃに対し素
であろう。

• 命題７ー２４（２数に素なら積にも素）
  による。
• 　Ａ×Ｂ;(互いに素)Ｃ
  となっている。

ところが
　Ａ、Ｂの積はＥである。

• 命題の設定２による。
• 　Ｅ;Ａ×Ｂ
  となっている。

それゆえ
　Ｅ、Ｃは互いに素である。

• 公理の補足２（命題７ー４）（約数・等分(倍数)での代入の原理）
  による。
• 　Ｅ;(互いに素)Ｃ
  となっている。

そうすれば
　同じ理由で
　Ｅ、Ｄも互いに素である。

• 命題の設定２ による。
• 　Ｅ;(互いに素)Ｄ
  となっている。

ゆえに
　Ｃ、Ｄの双方はＥに対し素である。

• 前節、前々節の結果による。
• 　(Ｃ、Ｄ);(互いに素)Ｅ
  となっている。

したがって
　Ｃ、Ｄの積もＥに対し素
であろう。

• 命題７ー２４（２数に素なら積にも素）
  による。
• 　Ｃ×Ｄ;(互いに素)Ｅ
  となっている。

ところが
　Ｃ、Ｄの積はＦである。

• 命題の設定２ による。
• 　Ｆ;＝Ｃ×Ｄ
  となっている。

よって
　Ｅ、Ｆは互いに素である。

• 公理の補足２（命題７ー４）（約数・等分(倍数)での代入の原理）
  による。
• 　Ｅ;(互いに素)Ｆ
  となっている。

これが証明すべきことであった。

• 命題７ー２６は、
  　任意の数Ａ、Ｂ
  に対し、
  　数Ｃ[;;(互いに素)(Ａ、Ｂ)]、
  　数Ｄ[;;(互いに素)(Ａ、Ｂ)]
  をとれば、
  　Ａ×Ｂ;(互いに素)Ｃ×Ｄ
  のことである。
  
• 命題７ー２６は推論用命題である。

  前提	作図	推論
  定義		7-16
  公準
  公理		補2(題7-4)
  命題		7-24
  その他	コ4(題7-1),コ(題7-24)

前 　　 次 　　 目次 　　頁頭