ユークリッド原論をどう読むか(9504)
頁末
前
次
目次
ユークリッド原論
第5巻
命題5ー4(同じ比の項の同数倍)
[任意の]同数倍
同じ比をもつ線分の作図(仮想的)
もし
第1の量が第2に対し、
第3が第4に対すると
同じ比をもつならば、
第1と第3の同数倍は
第2と第4の同数倍に対して、
何倍されようとも
同順にとられるとき、
同じ比をもつであろう。
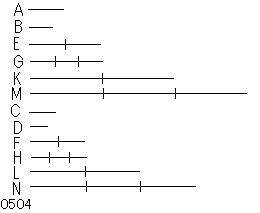
第1の量Aが
第2のBに対し、
第3のCが
第4のDに対すると
同じ比をもつとし、
A[、]Cの[任意の]同数倍E、Fと
B、Dの他の任意の同数倍G、Hが
とられたとせよ。
-
任意の比の作図は、
原理的には、命題6ー2(三角形の辺の平行線による辺の比例区分)
命題としては、命題6ー10(作図.線分の区分)
まで待たねばならない。
量の倍の場合を手掛かりにして、
定義5ー5(同じ比)
を構成し、
同じ比をもつ線分の作図を
命題の補足(定義5ー2)(作図.倍量)
における量の倍により可能な範囲で行い、
「同じ比をもつとし」と
仮想的な命題の設定をして、
以降の理論構成をしている。
(以下、コメント2(命題5ー4)(同じ比をもつ線分の作図(仮想的))という。)
-
量の倍は、命題の補足(定義5ー2)(作図.倍量)
による。
-
A:B=C:D、
E=mA、
F=mC、
G=nB、
H=nD
をとっている。
EがGに対するように、
FがHに対する
と主張する。
E、Fの[任意の]同数倍K、Lと
G、Hの他の任意の同数倍M、Nとが
とられたとせよ。
【・・・(a)】
- E:FとG:Hが
同じ比かどうか、
定義5ー5(同じ比)
に基づいて
判定しようとしている。
推論の設定である。
-
定義5ー5(同じ比)
に基づいて
同じ比かどうか判定する場合、
一方の任意の同数倍と
他方の任意の同数倍と
を比較するのが正当である。
したがって
前者にも「任意の」が記述されなばならない。
(以下、コメント(命題5ー4)([任意の]同数倍)という。)
-
K=pE、
L=pF、
M=qG、
N=qH
をとっている。
EはAの、
FはCの同数倍であり、
- 命題の設定
による。
-
E=mA、
F=mC、
となっている。
E、Fの同数倍K、Lがとられたから、
- (a)
による。
-
K=pE、
L=pF、
となっている。
KはAの、
LはCの
同数倍である。
【・・・(1)】
同じ理由で
MはBの、
NはDの
同数倍である。
【・・・(2)】
そして
AがBに対するように、
CはDに対し、
- 命題の設定 による。
-
A:B=C:D
となっている。
しかも
A、Cの同数倍K、Lと
B、Dの他の任意の同数倍M、Nが
とられたから、
- (1)
(2)
による。
-
K=pmA、
L=pmC、
M=qnB、
N=qnD
となっている。
もし
KがMより大きければ、LはNより大きく、
等しければ、等しく、
小さければ小さい。【・・・(3)】
- 命題の設定 、定義5ー5(同じ比)
による。
-
K(<,=,>)M
ならば
L(<,=,>)N
となっている。
そして
K、Lは
E、Fの同数倍であり、
M、Nは
G、Hの他の任意の同数倍である。
- (a)
による。
-
K=pE、
L=pF、
M=qG、
N=qH
となっている。
したがって
EがGに対するように、
FがHに対する。
よってもし
第1の量が第2に対し、
第3が第4に対すると
同じ比をもつならば、
第1と第3の同数倍は
第2と第4の同数倍に対して、
何倍されようとも同順にとられるとき、
同じ比をもつであろう。
これが証明すべきことであった。
- 命題5ー4は、
A:B=C:D
なら
mA:nB=mC:nD
のことである。
- 命題5ー4は推論用命題である。
前
次
目次
頁頭
