ユークリッド原論をどう読むか(11)
頁末
前
次
目次
ユークリッド原論
第7巻
命題7ー24(2数に素なら積にも素)
(互いに素な3個以上の数は仮想的)
もし
2つの数が
任意の数に対して素である
ならば、
それらの積も
同じ数に対して素
であろう。
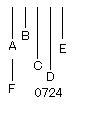
2数A、Bが
任意の数Cに対し素である
とし、
AがBにかけてDをつくる
とせよ。
-
「数(について)・・・とせよ」は、
コメント4(命題7ー1)
参照のこと。
-
命題7ー23の補足2(構成.互いに素(最小数の比)の2数)
により、
(数A:数C);(最小数の比)
をとり、
数B(;;(互いに素)C)
としている。
D=A×B
をとっている。
なお、
最後の部分により、
現段階では、
互いに素な3個以上の数を
とるのは仮想的である。
(以下、コメント(命題7ー24)(互いに素な3個以上の数は仮想的)という。)
実際的にとるには
命題7ー32の補足(数の素因数分解の一意性)、
命題9ー20(素数は無数)
が要請されるので
命題9ー20の補足2(構成.互いに素な任意個の数)
まで待たねばならない。
C、Dは互いに素である
と主張する。
もし
C、Dが
互いに素でない
ならば、
何らかの数がC、Dを割り切る
であろう。
割り切る
とし、
それをE
とせよ。
[......(a)]
C、Aは
互いに素であり、
-
命題の設定である。
-
C(互いに素)D
となっている。
[何らかの]数Eが
Cを割り切る
から、
A、Eは
互いに素である。
[......(1)]
-
命題7ー23(互いに素な数の約数は互いに素)
による。
-
A(互いに素)E
となっている。
そこで
EがDを割った商に等しい個数の
単位が
Fのなかにある
とせよ。
[......(b)]
-
推論の設定(a)
による。
-
数F(;;個数(F,単位)=(商(D,E);=f))
をとっている。
そうすれば
FがDを割った商は
Eのなかにある単位の個数である。
-
命題7ー15(割る数と商のいれかえ)
による。
-
個数(E,単位)=(商(D,F);=e)
となっている。
ゆえに
Eは
FにかけてDをつくった。
-
E×F=D
となっている。
つまり、
FがE個でDとなる
ということである。
ところが
Aは
BにかけてDをつくった。
したがって
E、Fの積は
A、Bの積に等しい。
-
前節、前々節の結果、
公理1ー1(同じものに等しいものは等しい)
による。
-
E×F=A×D
となっている。
ところが
もし
外項の積が
内項の積に等しけれ
ば、
4つの数は比例する。
それゆえ
EがAに対するように、
BがFに対する。
[......(2)]
-
前々節の結果による。
-
E×Fを外項の積、
A×Bを内項の積
と見なしている。
-
E:A=B:F
となっている。
ところが
A、Eは【互いに】素であり、
-
(1)
による。
-
A(互いに素)E
となっている。
【互いに】素である数は【同じ比の】最小であり、
同じ比をもつ2数のうち
最小の数は
それらと同じ比をもつ2数を、
大きい数が大きい数を、
小さい数が小さい数を、
すなわち
前項が前項を、
後項が後項を割り切り
その商は
等しい。
-
命題7ー20
(同じ比なら最小のが割り切る)
のことである。
ゆえに
EはBを割り切る。
ところが
Cをも割り切る。
したがって
Eは
互いに素であるB、Cを割り切る
ことになる。
-
命題の設定、
前節、前々節の結果による。
-
E|(B、(C;(互いに素)B)
となっている。
これは不可能である。
ゆえに
いかなる数も
数C、Dを割り切らない
であろう。
よって
C、Dは互いに素である。
-
定義7ー13(互いに素)
による。
-
C(互いに素)D
となっている。
これが証明すべきことであった。
- 命題7ー24は、
C(互いに素)(A、B)
をとれば、
C(互いに素)A×B
のことである。
- 命題7ー24は推論用命題である。
前
次
目次
頁頭
