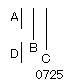ユークリッド原論をどう読むか（１１）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第７巻
　
命題７ー２５（対して素なら２乗も対して素）
もし
　２つの数が
　互いに素である
ならば、
　それらの１つの２乗は
　残りの数に対して素
であろう。

• 数は、 定義７ー２による。
• 互いに素は、 定義７ー１３による。
• ２乗は、 定義７ー１９の補足による。
• 対して素は、 定義の補足（命題７ー２３）による。

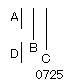
　Ａ、Ｂを互いに素である２数
とし、

• 「数（について）・・・とせよ」は、 コメント４（命題７ー１） 参照のこと。
• 　命題７ー２３の補足２(構成.互いに素(最小数の比)の２数)
  により、
  　(数Ａ：数Ｂ);(最小数の比)
  をとっている。
  

　Ａが２乗してＣをつくる
とせよ。

• Ａの２乗は、
  単位、Ａに対して
  命題６ー１１（作図.比例第３項）
  により、
  作図される比例第３項である。
  
• 　数Ｃ(;;＝正方(_Ａ))
  をとっている。

　Ｂ、Ｃは互いに素である
と主張する。

　ＤをＡに等しく
せよ。
　　　　　　[......(ａ)]

• 　Ｄ(;;＝Ａ)
  をとっている。

　Ａ、Ｂは
　互いに素であり、

• 命題の設定 による。
• 　Ａ(互いに素)Ｂ
  となっている。

　ＡはＤに等しい

• 推論の設定（ａ） による。
• 　Ａ＝Ｄ
  となっている。

から、
　Ｄ、Ｂも
　互いに素である。

• 命題７ー４の補足２ （約数・等分(倍数)での代入の原理）
  による。
• 　Ｄ(互いに素)Ｂ
  となっている。

それゆえ
　Ｄ、Ａの双方は
　Ｂに対し素である。

• 前節の結果、 命題の設定 による。
• 　Ｂ(互いに素)(Ｄ、Ａ)
  となっている。

ゆえに
　Ｄ、Ａの積も
　Ｂに対して素
であろう。

• 命題７ー２４（２数に素なら積にも素）
  による。
• 　Ｂ(互いに素)Ｄ×Ａ
  となっている。

ところが
　Ｄ、Ａの積は
　Ｃである。

• 命題の設定、 推論の設定（ａ） による。
• 　Ｃ＝Ｄ×Ａ
  となっている。

よって
　Ｃ、Ｂは互いに素である。

• 命題７ー４の補足２ （約数・等分(倍数)での代入の原理）
  による。
• 　Ｃ(互いに素)Ｂ
  となっている。

これが証明すべきことであった。

• 命題７ー２５は、
  　Ａ(互いに素)Ｂ
  ならば
  　正方(_Ａ)(互いに素)Ｂ
  のことである。
  
• 命題７ー２５は推論用命題である。

  前提	作図	推論
  定義
  公準
  公理
  命題	6-11,7-23補2	7-4補2,7-24
  その他	コ4(題7-1)

前 　　 次 　　 目次 　　頁頭