ユークリッド原論をどう読むか（１１）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第７巻
　
命題７ー２３（互いに素な数の約数は互いに素）
対して素
(構成.互いに素(最小数の比)の２数)
もし
　２つの数が互いに素である
ならば、
　それらの１つを割り切る数は
　残りの数に対して素
であろう。

• 数は、 定義７ー２による
• 互いに素は、 定義７ー１３による。
• 割り切るは、 定義５ー１の補足２ による。
• ＡがＢに対して素 とは、
  ＡとＢとが
  互いに素ということである。
  （以下、定義の補足（命題７ー２３） (対して素)とい。）
  「対して素」は、
  Ａに注目している表現で、
  「互いに素」は、
  ＡとＢとの関係に注目している表現である。
  

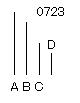
　 　Ａ、Ｂを
　互いに素である２つの数とし、
　何らかの数ＣがＡを割り切る
とせよ。

• 「数（について）・・・とせよ」は、
  コメント４（命題７ー１） 参照のこと。
• 　任意の数Ａ、Ｂ
  をとり、
  　命題７ー２２の補足(２数の比の最小数)
  により、
  　(数Ｘ：数Ｙ);＝Ａ：Ｂ、(最小数の比))
  をとり、
  改めて
  　Ａ、Ｂ
  として、溯って用いる。
  (以下、命題７ー２３の補足２(構成.互いに素(最小数の比)の２数)という。)
  さらに
  　数Ｃ(;;｜Ａ)
  としている。
  この部分により、
  現段階では、
  　Ａ、Ｂ、Ｃは仮想的である。

　Ｃ、Ｂも互いに素である
と主張する。

もし
　Ｃ、Ｂが互いに素でない
ならば、

• 背理法の仮定を述べようとしている。

　何らかの数がＣ、Ｂを割り切る
であろう。

• 背理法の仮定である。

　割り切るとし、
　それをＤ
とせよ。
　　　　　　[......(ａ)]

• 推論の設定である。
  
• 　Ｄ｜Ｃ、Ｄ｜Ｂ
  としている。
  

　ＤはＣを割り切り、
　ＣはＡを割り切る

• 前節、
  命題の設定
  による。
• 　Ｄ｜Ｃ、Ｃ｜Ａ
  となっている。

から、
　ＤもＡを割り切る。

• 命題７−１の補足（倍数の倍数、約数の約数）
  による。

ところが
　Ｂをも割り切る。

• 推論の設定（Ａ）
  による。
• 　Ｄ｜Ｂ
  となっている。

それゆえ
　Ｄは互いに素であるＡ、Ｂを割り切る
ことになる。

• 前節、前々節の結果による。
• 　Ｄ｜(Ａ、Ｂ)
  となっている。

　これは不可能である。

• 定義７ー１３（互いに素）
  に反する。

ゆえに
　いかなる数も
　数Ｃ、Ｂを割り切らない
であろう。

• 背理法による。

よって
　Ｃ、Ｂは互いに素である。

• 　Ｃ(互いに素)Ｂ
  となっている。

　これが証明すべきことであった。

• 命題７ー２３は、
  　数Ａ(互いに素)数Ｂ、
  　数Ｃ｜Ａ
  をとれば、
  　Ｃ(互いに素)Ｂ
  のことである。
• 命題７ー２３は推論用命題である。

  前提	作図	推論
  定義		7-13
  公準
  公理
  命題		7-1補
  その他	コ4(題7-1)	背理法

前 　　 次 　　 目次 　　頁頭