ユークリッド原論をどう読むか(10)
頁末
前
次
目次
ユークリッド原論
第6巻
命題6ー30(作図.外中比)
与えられた線分を
外中比に分けること。
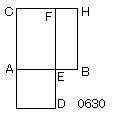
与えられた線分をABとせよ。
このとき
線分ABを
外中比に分けねばならぬ。
AB上に正方形BCが描かれ、
【・・・(a)】
-
命題1−46(作図.線分上に正方形)
による。
-
正方BC(_AB)
をとっている。
そして
AC上にBCに等しく、
BCに相似な図形ADだけはみでる
平行四辺形CDがつくられたとせよ。
【・・・(b)】
-
命題6ー29(作図.線分の平行四辺形外分割(コ))
による。
-
矩形CGDF(_CA(+)AG
;;=正方BC
,≡矩形CE(+)正方AD;∽正方BC)
となっている。
ところが
BCは正方形である。
したがって
ADも正方形である。
-
命題6ー21(同じ直線図形に相似な図形)
による。
-
AD;正方形
となっている。
そして
BCはCDに等しいから、
-
(b)による。
-
正方BC=矩形CD
となっている。
双方からCEが引き去られたとせよ。
そうすれば
残りのBFは残りのADに等しい。
-
公理1ー3(等しいものから等しいものをひく)
による。
-
矩形BF=正方BF
となっている。
しかも
等角でもある。
-
BF、ADともに、
4つの角すべてが直角である。
定義の補足(命題4ー2)(等角)
による。
-
矩形DF(等角)正方AD
となっている。
ゆえに
BF、ADの等角[等しい角]をはさむ辺は
逆比例する。
したがって
FEがEDに対するように、
AEがEBに対する。
そして
FEはABに、
EDはAEに等しい。
-
(a),(b)
による。
-
FE=AB、
ED=AE
となっている。
それゆえ
BAがAEに対するように、
AEはEBに対する。
-
命題5ー7(同一量の比)、
命題5ー11(同一の比に同じ比)
による。
BA:AE=AE:EB
となっている。
そして
ABはAEより大きい。
-
背理法の仮定として、
AEがABに等しい、
または、
より大きいとすれば、
公理1ー8(大きい)
により
BCよりCDが大きくなり、
(b)
に矛盾する。
よって
ABはAEより大きい。
-
AB>AE
となっている。
ゆえに
AEもEBより大きい。
-
定義5ー5(同じ比)
による。
-
AE>EB
となっている。
よって
線分ABは
Eにおいて外中比に分けられ、
そして
その大きい部分はAEである。
これが作図すべきことであった。
- 作図としては、
命題2ー11(作図.線分の混合分割)
と同じであり、
その作業としては、
命題2ー11(作図.線分の混合分割)
の方が
圧倒的に簡単である。
- 命題6ー30は、
線分AB
に対して、
矩形CGDF(_CA(+)AG
;;=正方BC
,≡矩形CE(+)正方AD;∽正方BC)
をとれば、
AB:AE=AE:EB(外中比)
のことである。
- 命題6ー30は作図用命題である。
前
次
目次
頁頭
