ユークリッド原論をどう読むか（１０）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第６巻

命題６ー２１（同じ直線図形に相似な図形）
同じ直線図形に相似な図形はまた
　互いに相似である。

• 直線図形は、 定義１ー１９ による。
• 相似は、 定義６ー１ による。
• 図形は、 定義１ー１４ による。

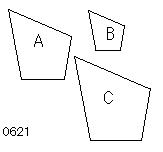
直線図形Ａ、Ｂの双方が
　Ｃに相似であるとせよ。

• 命題６ー１８（作図.線分上に相似な直線図形）
  による。
• 　直線図形Ｃ
  に対して、
  　直線図形Ａ[∽Ｃ]、
  　直線図形Ｂ[∽Ｃ]
  をとっている。
  　∠ＤＥＦ,Ｃ、∠ＤＥＦ,Ａ、
  　∠ＤＥＦ,Ｂ
  が対応している。
  

Ａはまた
　Ｂに相似であると主張する。
　
Ａは
　Ｃに相似であるから、
　それと等角であり、
　等しい角をはさむ辺は比例する。

• 定義６ー１（相似）
  による。
• 　∠ＤＥＦ,Ａ＝∠ＤＥＦ,Ｃ
  　ＤＥ,Ａ：ＥＦ,Ａ＝ＤＥ,Ｃ：ＥＦ,Ｃ
  となっている。

また
　Ｂは
　Ｃに相似であるから、
　それと等角であり、
　等しい角をはさむ辺は比例する。

• 定義６ー１（相似）
  による。
• 　∠ＤＥＦ,Ｂ＝∠ＤＥＦ,Ｃ
  　ＤＥ,Ｂ：ＥＦ,Ｂ＝ＤＥ,Ｃ：ＥＦ,Ｃ
  

それゆえ
　Ａ、Ｂの双方はＣと等角であり、
　等しい角をはさむ辺は比例する。

• 定義６ー１（相似）
  により、
  　Ａの任意の角は
  　それと対応する等しいＣの角があり、
  　それぞれの角をはさむ辺は比例し、
  　そのＣの角と対応する等しいＢの角があり、
  　それぞれの角をはさむ辺は比例する。
  公理１ー１（同じものに等しい）、
  命題５ー１１（同一の比に同じ比）
  により、
  　Ａの任意の角は
  　それと対応する等しいＢの角と等しく、
  　それぞれの角をはさむ辺は比例する。
  　ということである。
• 　∠ＤＥＦ,Ａ＝∠ＤＥＦ,Ｂ
  　ＤＥ,Ａ：ＥＦ,Ａ＝ＤＥ,Ｂ：ＥＦ,Ｂ
  となっている。

よって
　ＡはＢに相似である。

• 定義６ー１（相似）
  による。
• 　Ａ∽Ｂ
  となっている。

これが証明すべきことであった。

• 命題６ー２１は、
  　直線図形Ｃ
  に対して、
  　直線図形Ａ[∽Ｃ]、
  　直線図形Ｂ[∽Ｃ]
  をとれば、
  　Ａ∽Ｂ
  のことである。
• 命題６ー２１は推論用命題である。

  前提	作図	推論
  定義		6-1
  公準
  公理		1-1
  命題	6-18	5-11
  その他

前 　　 次 　　 目次 　　頁頭