ユークリッド原論をどう読むか（５）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論

第２巻

命題２ー１１（作図.線分の混合分割）
　与えられた線分を２分し、
　全体と一つの部分とにかこまれた矩形を
　残りの部分の上の正方形に
　等しくする
こと。

• 線分は、定義の補足（命題１ー１）による。
• かこまれたは、定義２ー１による。
• 矩形は、定義１ー２２による。
• 正方形は、定義１ー２２による。
• 等しいは、公理１ー７による。

　ＡＢを与えられた線分
とせよ。

• 　線分ＡＢ
  をとっている。

このとき
　ＡＢを２分し、
　全体と一つの部分とにかこまれた矩形を
　残りの部分の上の正方形に
　等しくしなければならぬ。


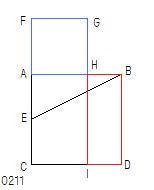
　ＡＢ上に正方形ＡＣＤＢが描かれ、
　　　　　　【・・・(a)】

• 　命題１ー４６（作図.線分上に正方形）
  による。
• 　正方ＡＣＤＢ(_ＡＢ)
  をとっている。

　ＡＣが点Ｅにおいて２等分され、
　　　　　　[......(b)]

• 　命題１ー１０作図・線分の２等分）
  による。
• 　Ｅ；中点（ＡＣ）
  をとる。

　ＢＥが結ばれ、

• 　公準１ー１（作図.直線）
  による。

　ＣＡがＦまで延長上され、

• 　公準１ー２（作図.直線の延長）
  による。
• 　Ｆ；点[延長ＣＡ]
  をとっている。

　ＥＦがＢＥに等しくされ、
　　　　　　【・・・(c)】

• 　ＣＡを延長しておいて、
  　命題１ー３の補足（作図.等しい線分となる点）
  により、
  　ＥからＢＥに等しくなるところに点をとり、
  　それをＦ
  とする。
• 　Ｆ'；点（ＣＦ;;ＥＦ'＝ＢＥ）
  をとり、
  　Ｆ'をＦと改める。

　ＡＦ上に正方形ＦＨ［すなわちＡＦＧＨ］が描かれ、
　　　　　　【・・・(d)】

• 　命題１ー４６（作図.線分上に正方形）
  による。
• 　正方ＦＨ(_ＡＦ)
  をとっている。

　ＧＨがＩまで延長された
とせよ。

• 　公準１ー２（作図.直線の延長） 、
  　命題１ー３０の補足(交線に平行な線)
  により
  　直線ＧＨはＣＤと交わる。
  　その交点をＩ
  としている。
• 　Ｉ；交点（直線ＧＨ、辺ＣＤ）
  をとる。

　ＡＢ
は
　Ｈにおいて分けられ、
　ＡＢ、ＢＨにかこまれた矩形《を》［が］
　ＡＨ上の正方形に等しく《する》［なる］
と主張する。
　
　線分ＡＣ
は
　Ｅで２等分され、
　ＦＡがそれに加えられる

• 　(b) 、(c) による。
• 　Ｅ；中点（ＡＣ）、
  　ＦＣ＝ＡＣ＋ＦＡ
  となっている。
  

から、
　ＣＦ、ＦＡにかこまれた矩形［ＣＦＧＨ］と
　ＡＥ上の正方形との和
は
　ＥＦ上の正方形に等しい。

• 　前節、
  　命題２ー６（線分の矩形外分割）
  による。
• 　矩形(ＣＦ、ＦＡ)＋正方(_ＡＥ)＝正方(_ＥＦ)
  となっている。
  

そして、
　ＥＦ
は
　ＥＢに等しい。

• 　(c) による。
• 　ＥＦ＝ＥＢ
  となっている。
  

それゆえ
　矩形ＣＦ、ＦＡとＡＥ上の正方形との和
は
　ＥＢ上の正方形に等しい。

• 　前節、前々節、
  　定義１ー２２（正方形・矩形・菱形・長斜方形・トラペジオン）、
  　公理１ー２（等しいものに等しいものを加える）
  による。
• 　矩形(ＣＦ、ＦＡ)＋正方(_ＡＥ)＝正方(_ＥＢ)
  となっている。
  

ところが
　Ａにおける角
は
　直角である

• (a) による。
• 　∠ＥＡＢ＝∠Ｒ
  となっている。
  

　ＢＡ、ＡＥ上の正方形の和
は
　ＥＢ上の正方形に等しい。

• 　前節、
  　命題１ー４７（三平方の定理）
  による。
• 　正方(_ＢＡ)＋正方(_ＡＥ)＝正方(_ＥＢ)
  となっている。
  

［したがって
　矩形ＣＦ、ＦＡとＡＥ上の正方形との和
は
　ＢＡ、ＡＥ上の正方形の和に等しい。］

• 　前節、前々々節、
  　公理１ー１（同じものに等しい）
  による。
• この部分がないと次の論理につながらない。
• 　矩形(ＣＦ、ＦＡ)＋正方(_ＡＥ)＝正方(_ＢＡ)＋正方(_ＡＥ)
  となっている。
  

　双方から
　ＡＥ上の正方形がひかれた
とせよ。
そうすれば
　残りのＣＦ、ＦＡにかこまれた矩形
は
　ＡＢ上の正方形に等しい。
　　　　　　【・・・(1)】

• 　前節、
  　公理１ー３（等しいものから等しいものをひく）
  による。
• 　矩形(ＣＦ、ＦＡ)＝正方(_ＢＡ)
  となっている。
  

そして
　ＡＦはＦＧに等しい

• 　(d)による。
• 　ＡＦ＝ＦＧ
  となっている。
  

から、
　矩形ＣＦ、ＦＡ
は
　［矩形］ＦＩである。

• 　前節、
  　定義２ー１（かこまれる）
  による。
• 　矩形(ＣＦ、ＦＡ)＝矩形(ＦＩ)
  となっている。
  

ところが
　ＡＢ上の正方形
は
　［矩形］ＡＤである。

• 　(a)による。
• 　正方(_ＡＢ)＝矩形(ＡＤ)
  となっている。
  

それゆえ
［矩形］ＦＩは
　［矩形］ＡＤに等しい。

• 　前節、前々節、 (1)、
  　公理１ー１（同じものに等しい）
  による。
• 　矩形(ＦＩ)＝正方(ＡＤ)
  となっている。
  

　双方から
　［矩形］ＡＩがひかれた
とせよ。
そうすれば
　残りの［矩形］ＦＨ
は
　［矩形］ＨＤに等しい。
　　　　　　【・・・(2)】

• 　前節、(1)、
  　公理１ー３（等しいものから等しいものをひく）
  による。
• 　矩形(ＨＦ)＝矩形(ＨＤ)
  となっている。
  

そして、
　ＡＢ
は
　ＢＤに等しい

• 　(a) による。
• 　ＡＢ＝ＢＤ
  となっている。
  

から、
　［矩形］ＨＤ
は
　矩形ＡＢ、ＢＨに等しい。

• 　前節、
  　定義２ー１（かこまれる）
  による。
• 　矩形(ＨＤ)＝矩形(ＡＢ、ＢＨ)
  となっている。
  

ところが
［矩形］ＦＨは
　ＡＨ上の正方形である。

• 　(d) による。
• 　矩形(ＦＨ)；正方(_ＡＨ)
  となっている。
  

したがって
ＡＢ、ＢＨにかこまれた矩形は
　ＨＡ上の正方形に等しい。

• 　前節、前々節、(2)、
  　公理１ー１（同じものに等しい）
  による。
• 　矩形(ＡＢ、ＢＨ)＝正方(_ＨＡ)
  となっている。
  

よって
　与えられた線分ＡＢは
　Ｈにおいて分けられ、
　ＡＢ、ＢＨにかこまれた矩形を
　ＨＡ上の正方形に等しくする。
　

• 　前節による。
• 　Ｈ；点（ＡＢ、矩形(ＡＨ、ＨＢ)＝正方(_ＨＡ)）
  となっている。
  

これが作図のすべきものであった。

• 　線分ＡＢ
  に対して、
  　正方ＡＢＤＣ＝正方(_ＡＢ)、
  　Ｅ；中点（ＡＣ）、
  　Ｆ；点（延長ＣＡ;;ＥＦ＝ＢＥ）、
  　正方ＡＦＧＨ(_ＡＦ)
  をとるならば、
  　矩形(ＡＢ、ＢＨ)＝正方(_ＡＨ)
  のことである。
  
• 命題2-11は作図用命題である。
  

  前提	作図	推論
  定義		1-22,2-1
  公準	1-1,1-2
  公理		1-1, 1-2,1-3
  命題	1-3補,1-10,1-30補,1-46	1-47,2-6
  その他

前 　　 次 　　 目次 　　頁頭