ユークリッド原論をどう読むか（１０）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第６巻

命題６ー３１（直角三角形の辺上の相似な図形）
直角三角形において
　直角に対する辺の上の図形は
　直角をはさむ２辺の上の
　相似でかつ相似な位置に描かれた
　図形の和に等しい。

• 直角三角形は、 定義１ー２１ による。
• 直角は、 定義１ー１０ による。
• 辺は、 定義１ー１９の補足 による。
• 図形は、 定義１ー１４ による。
• 相似は、 定義６ー１ による。
• 相似な位置は、 定義の補足（命題６ー１８） による。
• 等しいは、 公理１ー７ による。

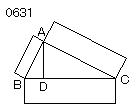
ＡＢＣを
　角ＢＡＣが直角である直角三角形とせよ。

• 　線分ＡＢ、
  　点Ｃ[;;∠ＢＡＣ＝∠Ｒ]、
  　△ＡＢＣ
  をとっている。

ＢＣ上の図形は
　ＢＡ、ＡＣ上の
　相似でかつ相似な位置に描かれた
　図形の和に等しい
　と主張する。
　

• 相似でかつ相似な位置に図形を描くのは
  命題６ー１８（作図.線分上に相似な直線図形）
  による。
  ここでの図は、
  　相似でかつ相似な位置にある
  　長方形であるが、
  　証明そのものは
  　一般の直線図形において通用する。
  なお、
  　本命題が、
  　相似でかつ相似な位置にあるとされる例で、
  　対応する辺が
  　平行でないものの最初である。
  

垂線ＡＤが下されたとせよ。

• 命題１ー１２（作図・線分への垂線）
  による。
• 　点Ｄ(ＢＣ;;∠ＡＤＣ＝∠Ｒ)
  をとっている。

そうすれば
　直角三角形ＡＢＣにおいて
　Ａにおける直角から
　底辺ＢＣに垂線ＡＤが下された

• 　ＡＤ⊥ＢＣ
  となっている。

から、
　垂線上の三角形ＡＢＤ、ＡＤＣは
　全体ＡＢＣに対しても互いに相似である。

• 命題６ー８（直角三角形の垂線と相似）
  による。
• 　△ＡＢＤ∽△ＡＤＣ∽ＡＢＣ
  となっている。

そして
　ＡＢＣは
　ＡＢＤに相似であるから、
　ＣＢがＢＡに対するように
　ＡＢがＢＤに対する。

• 定義６ー１（相似）
  による。
• 　ＣＢ：ＢＡ＝ＡＢ：ＢＤ
  となっている。

そして
　３線分が比例するから、
　第１の線分が第３に対するように
　第１の上の図形が
　第２の上の相似でかつ相似な位置に描かれた
　図形に対する。

• 命題６ー１９（相似な三角形の比は辺の比の２乗）、
  定義５ー９（２乗の比）
  による。

それゆえ
　ＣＢがＢＤに対するように、
　ＣＢ上の図形が
　ＢＡ上の相似でかつ相似な位置に描かれた
　図形に対する。

• 　ＣＢ：ＢＤ
  　＝直線図形Ｅ(_ＣＢ)：直線図形Ｇ(_ＡＢ;;∽∽直線図形Ｅ)
  となっている。

同じ理由で
　ＢＣがＣＤに対するように、
　ＢＣ上の図形がＣＡ上の図形に対する。

• 　ＢＣ：ＣＤ
  　＝直線図形Ｅ(_ＢＣ)：直線図形Ｆ(_ＡＢ;;∽∽直線図形Ｅ)
  となっている。

ゆえに
　ＢＣがＢＤ、ＤＣの和に対するように、
　ＢＣ上の図形が
　ＢＡ、ＡＣ上の相似でかつ相似な位置に描かれた
　図形の和に対する。

• 命題５ー２４（各量の同じ比の和は同じ比）
  による。
• 　ＢＣ：ＢＤ＋ＤＣ
  　＝直線図形Ｅ(;_ＢＣ)
  　　：直線図形Ｆ(;_ＢＡ)＋直線図形Ｇ(;_ＡＣ)
  となっている。

ところが
　ＢＣはＢＤ、ＤＣの和に等しい。

• 公理１ー７（等しい）
  による。
• 　ＢＣ＝ＢＤ＋ＤＣ
  となっている。

したがって
　ＢＣ上の図形も
　ＢＡ、ＡＣ上の相似でかつ相似な位置に描かれた
　図形の和に等しい。

• 定義５ー５（同じ比）
  による。
• 　直線図形Ｅ(;_ＢＣ)
  　＝直線図形Ｆ(;_ＢＡ)＋直線図形Ｇ(;_ＡＣ)
  となっている。

よって
　直角三角形において
　直角に対する辺の上の図形は
　直角をはさむ２辺の上の
　相似でかつ相似な位置に描かれた
　図形の和に等しい。
これが証明すべきことであった。

• 命題６ー３１は、
  　△ＡＢＣ[;;∠ＢＡＣ＝∠Ｒ]
  に対して、
  　直線図形Ｅ(;_ＢＣ)
  　＝直線図形Ｆ(;_ＢＡ)＋直線図形Ｇ(;_ＡＣ)
  のことである。
• 命題６ー３１は推論用命題である。

  前提	作図	推論
  定義		5-5,5-9,6-1
  公準
  公理		1-7
  命題	1-12	5-24,6-8,6-19
  その他

前 　　 次 　　 目次 　　頁頭