ユークリッド原論をどう読むか（１０）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第６巻

命題６ー１９（相似な三角形の比は辺の比の２乗）
（系.比例３線分と第１、２上の相似な図形）
相似な三角形は
　互いに対応する辺の比の
　２乗の比をもつ。

• 相似は、 定義６ー１ による。
• 三角形は、 定義１ー１９の補足２ による。
• 辺は、 定義１ー１９の補足 による。
• 比は、 定義５ー３ による。
• ２乗の比は、 定義５ー９ による。

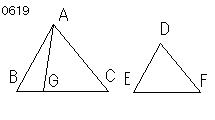
ＡＢＣ、ＤＥＦを
　Ｂにおける角がＥにおける角に等しく、
　ＡＢがＢＣに対するように、
　ＤＥがＥＦに対し、
　ＢＣがＥＦに対応する
　相似な三角形とせよ。

• 命題６ー６の補足（作図.２辺が比例し挟角が等しい三角形）
  による。
• 　△ＡＢＣ、ＤＥ
  に対して、
  　Ｆ(同向側(ＤＥ,ＡＢ,Ｃ)
  　　;;∠ＤＥＦ＝∠ＡＢＣ,ＡＢ：ＢＣ＝ＤＥ：ＥＦ)
  　△ＤＥＦ
  をとっている。

三角形ＡＢＣは
　三角形ＤＥＦに対し、
　ＢＣがＥＦに対する比の２乗の比をもつ
　と主張する。

ＢＣ、ＥＦの第３の比例項ＢＧがとられ、
　ＢＣがＥＦに対するように、
　ＥＦがＢＧに対するとせよ。 【・・・(a)】

• 命題６ー１１（作図.比例第３項）
  により、
  　第３比例項Ｂ'Ｇ'を作図し、
  命題１ー３の補足（作図.等しい線分となる点）
  により、
  　Ｇを、
  　線分ＢＣ上に、
  　ＢＧがＢ'Ｇ'に等しくなるようにとる。
• 　点Ｇ(ＢＣ;;ＢＣ：ＥＦ＝ＥＦ：ＢＧ)
  をとっている。

そして
　ＡＧが結ばれたとせよ。

• 公準１ー１（作図.直線）
  による。
• 　線分ＡＧ
  をとっている。

そうすれば
　ＡＢがＢＣに対するように、
　ＤＥがＥＦに対するから、

• 命題の設定、 定義６ー１（相似）
  による。
• 　ＡＢ：ＢＣ＝ＤＥ：ＥＦ
  となっている。

　いれかえて
　ＡＢがＤＥに対するように、
　ＢＣがＥＦに対する。

• 命題５ー１６（比例すれば錯比も比例）
  による。
• 　ＡＢ：ＤＥ＝ＢＣ：ＥＦ
  となっている。

ところが
　ＢＣがＥＦに対するように、
　ＥＦがＢＧに対する。

• (a) による。
• 　ＢＣ：ＥＦ＝ＥＦ：ＢＧ
  となっている。

それゆえ
　ＡＢがＤＥに対するように
　ＥＦがＢＧに対する。

• 命題５ー１１（同一の比に同じ比）
  による。
• 　ＡＢ：ＤＥ＝ＥＦ：ＢＧ
  となっている。

ゆえに
　三角形ＡＢＧ、ＤＥＦの
　等しい角をはさむ辺は
　反比例する。

• 定義６ー２（逆比例）
  による。
• 　(ＡＢ,ＢＧ)(反比例)(ＤＥ,ＥＦ)
  となっている。

ところが
　１つの角を等しくし、
　《等角》［等しい角］を
　　はさむ辺が反比例する
　２つの三角形は
　等しい。

• 命題６ー１５（等積で１角の等しい三角形と逆比例）
  による。

したがって
　 三角形ＡＢＧは
　三角形ＤＥＦに等しい。 【・・・(1)】

• 　△ＡＢＧ＝△ＤＥＦ
  となっている。

そして
　ＢＣがＥＦに対するように、
　ＥＦがＢＧに対し、

• (a) による。
• 　ＢＣ：ＥＦ＝ＥＦ：ＢＧ
  となっている。

　しかももし
　３線分が比例するならば、
　第１は第３に対し、
　第２に対する比の２乗の比をもつから、

• 定義５ー９（２乗の比）
  による。

　ＢＣは
　ＢＧに対し、
　ＣＢがＥＦに対する比の２乗の比をもつ。

• 　ＢＣ：ＢＧ＝(ＣＢ：ＥＦ)^2
  となっている。

ところが
　ＣＢがＢＧに対するように、
　三角形ＡＢＣが三角形ＡＢＧに対する。

• 命題６ー１（同高の三角形、平行四辺形は底辺と比例）
  による。
• 　ＣＢ：ＢＧ＝△ＡＢＣ：△ＡＢＧ
  となっている。

それゆえ
　三角形ＡＢＣは
　ＡＢＧに対し、
　ＢＣがＥＦに対する比の２乗の比をもつ。

• (a ), 命題５ー１１（同一の比に同じ比）
  による。
• 　△ＡＢＣ：△ＡＢＧ＝(ＢＣ：ＥＦ)^2
  となっている。

ところが
　三角形ＡＢＧは
　三角形ＤＥＦに等しい。

• (1)による。
• 　△ＡＢＧ＝△ＤＥＦ
  となっている。

したがって
　三角形ＡＢＣは
　三角形ＤＥＦに対し、
　ＢＣがＥＦに対する比の２乗の比をもつ。

• 命題５ー１１（同一の比に同じ比）
  による。
• 　△ＡＢＣ：△ＤＥＦ＝(ＢＣ：ＥＦ)^2
  となっている。

よって
　相似な三角形は
　互いに対応する辺の比の２乗の比をもつ。
系
これから
　次のことが明らかである、
　すなわち
　 もし
　３線分が比例するならば、
　第１が第３に対するように、
　第１の上に描かれた図形が
　第２の上に描かれた
　相似でかつ相似な位置にある図形に対する。
（以下、命題６ー１９の系（系.比例３線分と第１、２上の相似な図形） という。）

　定義５ー９（２乗の比）
による。
• 　Ａ：Ｂ＝Ｂ：Ｃ
  ならば、
  　図形Ｄ[_Ａ]：図形Ｅ(∽図形Ｄ,_Ｂ)
  　＝Ａ：Ｃ
  のことである。

これが証明すべきことであった。

• 命題６ー１９は、
  　△ＡＢＣ
  に対して、
  　△ＤＥＦ[∽△ＡＢＣ
  　　;;∠Ｂ＝∠Ｅ,ＡＢ：ＢＣ＝ＤＥ：ＥＦ]
  ならば、
  　△ＡＢＣ：△ＤＥＦ＝(ＢＣ：ＥＦ)^2
  のことである。
• 命題６ー１９の系（系.比例３線分と第１、２上の相似な図形）

  前提	作図	推論
  定義		5-9
  公準
  公理
  命題		6-19
  その他

• 命題６ー１９は推論用命題である。

  前提	作図	推論
  定義		5-9,6-1,6-2
  公準	1-1
  公理
  命題	1-3補,6-6補,6-11	5-11,5-16,6-1,6-15
  その他

前 　　 次 　　 目次 　　頁頭