ユークリッド原論をどう読むか（１０）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第６巻

命題６ー１８（作図.線分上に相似な直線図形）
相似な位置
与えられた線分上に
　与えられた直線図形に相似で
　かつ
　相似な位置にある
　直線図形を描くこと。

• 線分は、 定義の補足（命題１ー１） による。
• 直線図形は、 定義１ー１９ による。
• 相似は、 定義６ー１ による。
• 相似な位置は、
  　指定された２線分が
  　対応する辺となるような
  　相似関係の位置
  ということである。
  また、
  　対応する辺は平行になっている場合が多い。
  （以下、定義の補足（命題６ー１８）という。）

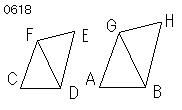
与えられた線分をＡＢ、
　与えられた直線図形をＣＥとせよ。

• 準一般的な証明である。
  直線図形は、
  　１つの頂点から
  　他の頂点へ対角線を引くことにより
  　三角形に分解できる。
  分解した三角形を、
  　１つずつ、
  　相似でかつ相似な位置に
  　描いてゆくことにより、
  　どのような直線図形であっても
  　相似なものを描くことができる。
  この作図の要点を
  　四角形を用いて示している。
  準一般的な証明は、
  　コメント２（命題５ー１）参照のこと。
• 　線分ＡＢ、
  　直線図形ＣＥ
  をとっている。

このとき
　線分ＡＢ上に
　直線図形ＣＥに相似で
　かつ
　相似な位置にある
　直線図形を描かねばならぬ。
　
ＤＦが結ばれたとし、

• 公準１ー１（作図.直線）
  による。
• 　対角線ＤＦ
  をとっている。

　 線分ＡＢ上に
　その上の点Ａ、Ｂにおいて
　Ｃにおける角に等しい角ＧＡＢと、
　角ＣＤＦに等しい角ＡＢＧがつくられたとせよ。 【・・・(a)】

• 命題１ー２３（作図・直線上に指定された角）
  により、
  　角ＧＡＢ、ＡＢＧ’をつくる。
  命題１ー１７（三角形の２角の和）
  により、
  　角ＦＣＤとＣＤＦとの和は
  　２直角より小さいから、
  公理１ー２（等しいものに等しいものを加える） 、
  公理１ー８の補足２（等より大・小、大・小に等）
  により、
  　角ＧＡＢとＡＢＧ’との和は
  　２直角より小さい。
  公準１ー５（平行線公準）
  により、
  　ＡＧとＡＧ’とが交わるから、
  　その交点を改めてＧとし、
  　遡って用いている。
• 　点Ｇ[同向側(ＢＡ,ＤＣ,Ｆ);;∠ＧＡＢ＝∠ＦＣＤ]、
  　点Ｇ'[同向側(ＡＢ,ＣＤ,Ｆ);;∠ＡＢＧ'＝∠ＣＤＦ]、
  　交点Ｇ"(ＡＧ,ＢＧ')、
  　Ｇ"＞＞Ｇ
  をとっている。

そうすれば
　残りの角ＣＦＤは
　角ＡＧＢに等しい。

• 命題６ー５の補足（２組の角が等しい三角形は他の角も等しい）
  による。
• 　∠ＣＦＤ＝∠ＡＧＢ
  となっている。

ゆえに
　 三角形ＦＣＤは
　三角形ＧＡＢに等角である。 【・・・(1)】

• 定義の補足（命題４ー２）(等角)
  による。
• 　△ＦＣＤ(等角)△ＧＡＢ
  となっている。

したがって
　［対応する辺が］
　比例し、
　 ＦＤがＧＢに対するように、
　ＦＣがＧＡに、
　ＣＤがＡＢに対する。 【・・・(2)】

• 命題６ー４の補足(等角三角形の対応辺の比例)
  による。
• 　ＦＤ：ＧＢ＝ＦＣ：ＧＡ＝ＣＤ：ＡＢ
  となっている。

また
　線分ＢＧ上に
　その上の点Ｂ、Ｇにおいて
　角ＤＦＥに等しい角ＢＧＨと、
　角ＦＤＥに等しい角ＧＢＨがつくられたとせよ。

2
• (a)と同様である。
• 　点Ｈ[同向側(ＢＧ,ＤＦ,Ｅ);;∠ＢＧＨ＝∠ＤＦＥ]、
  　点Ｈ'[同向側(ＧＢ,ＦＤ,Ｅ);;∠ＧＢＨ'＝∠ＦＤＥ]、
  　交点Ｈ"(ＧＨ,ＢＨ')、
  　Ｈ"＞＞Ｈ
  をとっている。

そうすれば
　残りのＥにおける角は
　残りのＨにおける角に等しい。

• 命題６ー５の補足（２組の角が等しい三角形は他の角も等しい）
  による。
• 　∠Ｅ＝∠Ｈ
  となっている。

ゆえに
　　 三角形ＦＤＥは
　三角形ＧＨＢに等角である。 【・・・(3)】

• 定義の補足（命題４ー２）(等角)
  による。
• 　△ＦＤＥ(等角)△ＧＨＢ
  となっている。

したがって
　比例し、
　ＦＤがＧＢに対するように、
　ＦＥがＧＨに、
　ＥＤがＨＢに対する。

• 命題６ー４の補足(等角三角形の対応辺の比例)
  による。
• 　ＦＤ：ＧＢ＝ＦＥ：ＧＨ
  　＝ＥＤ：ＨＢ
  となっている。

ところが
　ＦＤがＧＢに対するように、
　ＦＣがＧＡに、
　ＣＤがＡＢに対する
　ことが先に証明された。

• (2) による。
• 　ＦＤ：ＧＢ＝ＦＣ：ＧＡ
  　＝ＣＤ：ＡＢ
  となっている。

それゆえ
　 ＦＣがＡＧに対するように、
　ＣＤがＡＢに、
　ＦＥがＧＨに、
　また
　ＥＤがＨＢに対する。 【・・・(4)】

• 命題５ー１１（同一の比に同じ比）
  による。
• 　ＦＣ：ＡＧ＝ＣＤ：ＡＢ
  　＝ＦＥ：ＧＨ＝ＥＤ：ＨＢ
  となっている。

そして
　角ＣＦＤが角ＡＧＢに、
　角ＤＦＥが角ＢＧＨに等しいから、

• (1) (3) による。
• 　∠ＣＦＤ＝∠ＡＧＢ、
  　∠ＤＦＥ＝∠ＢＧＨ
  となっている。

　角ＣＦＥ全体は
　角ＡＧＨ全体に等しい。

• 公理１ー２（等しいものに等しいものを加える）
  による。
• 　∠ＣＦＥ＝∠ＡＧＨ
  となっている。

同じ理由で
　角ＣＤＥも角ＡＢＨに等しい。

• 　∠ＣＤＥ＝∠ＡＢＨ
  となっている。

ところが
　Ｃにおける角もＡにおける角に、
　Ｅにおける角もＨにおける角に等しい。

• (1) (3) による。
• 　∠Ｃ＝∠Ａ、
  　∠Ｅ＝∠Ｈ
  となっている。

ゆえに
　ＡＨはＣＥに等角である。

• 定義の補足（命題４ー２）(等角)
  による。
• 　直線図形ＡＨ(等角)直線図形ＣＥ
  となっている。

そして
　それらの等しい角をはさむ辺が比例する。

• (4) による。

したがって
　直線図形ＡＨは直線図形ＣＥに相似である。

• 定義６ー１（相似）
  による。
• 　直線図形ＡＨ(相似)直線図形ＣＥ
  となっている。

よって
　与えられた線分ＡＢ上に
　与えられた直線図形ＣＥに相似で
　かつ
　相似な位置にある
　直線図形ＡＨが描かれた。
これが作図すべきものであった。

• 命題６ー１８は、
  　線分ＡＢ、
  　直線図形ＣＥ
  に対して、
  　点Ｇ[同向側(ＢＡ,ＤＣ,Ｆ);;∠ＧＡＢ＝∠ＦＣＤ]、
  　点Ｇ'[同向側(ＡＢ,ＣＤ,Ｆ);;∠ＡＢＧ'＝∠ＣＤＦ]、
  　交点Ｇ"(ＡＧ,ＢＧ')、
  　Ｇ"＞＞Ｇ
  　点Ｈ[同向側(ＢＧ,ＤＦ,Ｅ);;∠ＢＧＨ＝∠ＤＦＥ]、
  　点Ｈ'[同向側(ＧＢ,ＦＤ,Ｅ);;∠ＧＢＨ'＝∠ＦＤＥ]、
  　交点Ｈ"(ＧＨ,ＢＨ')、
  　Ｈ"＞＞Ｈ
  をとれば、
  　直線図形ＡＨ(相似)直線図形ＣＥ
  のことである。
• 命題６ー１８は作図用命題である。

  前提	作図	推論
  定義		補(題4-2) ,6-1
  公準	1-1 ,1-5
  公理		1-2 ,1-8補
  命題	1-23	1-17 ,5-11 ,6-4補 ,6-5補
  その他

前 　　 次 　　 目次 　　頁頭