ユークリッド原論をどう読むか(9516)
頁末
前
次
目次
ユークリッド原論
第5巻
命題5ー16(比例すれば錯比も比例)
(同じ比の項の大等小2)
もし
4つの量が比例するならば、
《いれかえて》[錯比]も比例するであろう。
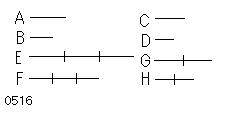
A、B、C、Dは
4つの比例する量であり、
AがBに対するように、
CがDに対するとせよ。
-
同じ比をもつ線分の作図(仮想的)は、
コメント2(命題5ー4)
参照のこと。
-
量A、B、C
を取り、
量D(;;A:B=C:D)
をとっている。
《いれかえて》[錯比]も比例し、
AがCに対するように
BがDに対するであろう
と主張する。
A、Bの[任意の]同数倍E、Fと
C、Dの別の任意の同数倍G、Hが
とられたとせよ。【・・・(a)】
- 推論の設定である。
- [任意の]同数倍は、コメント(命題5ー4)参照のこと。
-
(E、F)=m(A、B)、
(G、H)=n(C、D)
をとっている。
そうすれば、
EはAの、
FはBの同数倍であり、
-
倍数(E,A)=倍数(F,B)=m、
となっている。
約量は
それらの同数倍と同じ比をもつから、
AがBに対するように
EがFに対する。【・・・(a)】
- 命題5ー15(同数倍の比)
による。
-
A:B=E:F
となっている。
ところが
AがBに対するように、
CがDに対する。
- 命題の設定
である。
-
A:B=C:D
となっている。
それゆえ
CがDに対するように、
EがFに対する。【・・・(2)】
また、
G、Hは
C、Dの同数倍であるから、
- (a)による。
-
(G、H)=n(C、D)
となっている。
CがDに対するように、
GがHに対する。
- 命題5ー15(同数倍の比)
による。
-
C:D=G:H
となっている。
ところが
CがDに対するように、
EがFに対する。
ゆえに
EがFに対するように、
GがHに対する。【・・・(3)】
- 命題5ー15(同数倍の比)
による。
-
E:F=G:H
となっている。
ところがもし
4つの量が比例し、
第1の量が第3より大きければ、
第2も第4より大きく、
等しければ、
等しく、
小さければ、
小さいであろう。
したがってもし
EがGより大きければ、
FもHより大きく、
等しければ、
等しく、
小さければ、
小さい。【・・・(4)】
- (3)
、定義5ー6(比例)
による。
-
E(<、=、>)G
ならば、
F(<、=、>)H
となっている。
そして
E、FはA、Bの[任意の]同数倍であり、
G、HはC、Dの別の任意の同数倍である。
- (a)
による。
- [任意の]同数倍は、コメント(命題5ー4)参照のこと。
-
(E、F)=m(A、B)、
(G、H)=n(C、D)
となっている。
ゆえに
AがCに対するように、
BがDに対する。
よってもし
4つの量が比例するならば、
いれかえても比例するであろう。
これが証明すべきことであった。
-
一般に、
比例 A:B=C:D
において、
AとCは、
定義5ー4(比をもつ)
にいう
相互に比をもつ量である必要はない
が、
本定理においては、
相互に比をもつ量であること
が前提となる。
-
A:B=C:DかつA<=>Bなら
C<=>Dである
(以下、命題5ー16の補足(同じ比の項の大等小2)という。)
これは、
定義5ー5(同じ比)における同数倍を1倍としたものである。
- 命題5ー16は、
A:B=C:D
ならば、
A:C=B:D
のことである。
-
命題5ー16の補足(同じ比の項の大等小2)
| 前提 | 作図 | 推論 |
| 定義 |
|
5-5
|
| 公準 |
|
|
| 公理 |
|
|
| 命題 |
|
|
| その他 |
|
|
- 命題5ー16は推論用命題である。
前
次
目次
頁頭
