ユークリッド原論をどう読むか（２）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー１７（三角形の２角の和）
　すべての三角形において
　どの２角をとって
も
　その和は２直角より小さい。

• 　三角形は定義１ー１９の補足２による。
• 　角は定義１ー８による。
• 　直角は定義１ー１０による。
• 　小さいは公理１ー８の補足による。

　ＡＢＣを三角形
とせよ。

• 　三角形ＡＢＣ
  をとっている。

　三角形ＡＢＣのどの２角をとって
も
　その和は２直角より小さい
と主張する。

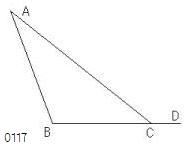
　ＢＣがＤまで延長された
とせよ。
　　　　　　【・・・(a)】

• 　公準１ー２（作図.直線の延長）
  による。
• 　点Ｄ[延長ＢＣ]
  をとっている。

そうすれば
　角ＡＣＤは
　三角形ＡＢＣの外角である
から、
　内対角ＡＢＣより大きい。

• 　命題１ー１６（外角と内対角）
  による。
• 　∠ＡＣＤ＞∠ＡＢＣ
  となっている。

　角ＡＣＢが双方に加えられた
とせよ。
そうすれば
　角ＡＣＤ、ＡＣＢの和は
　角ＡＢＣ、ＢＣＡの和より大きい。

• 　公理１ー４（不等なものに等しいものを加える）
  による。
• 　∠ＡＣＤ＋∠ＡＣＢ
  　＞∠ＡＢＣ＋∠ＢＣＡ
  となっている。

ところが
　角ＡＣＤ、ＡＣＢの和は２直角に等しい。

• 　(a) ,命題１ー１３（直線と２直角１）
  による。
• 　∠ＡＣＤ＋∠ＡＣＢ＝２×∠Ｒ
  となっている。

したがって
　角ＡＢＣ、ＢＣＡの和は
　２直角より小さい。

• 公理１ー８の補足２（等より大・小、大・小に等）
  による。
• 　∠ＡＢＣ＋∠ＢＣＡ＜２×∠Ｒ
  となっている。

同様にして
　角ＢＡＣ、ＡＣＢの和も、
　また
　角ＣＡＢ、ＡＢＣの和も
　２直角より小さい
ことを証明しうる。
　
よって
　すべての三角形において
　どの２角をとって
も
　その和は２直角より小さい。
　
　これが証明すべきことであった。

• 命題1-17は、
  　△ＡＢＣ
  において、
  　∠ＡＢＣ＋∠ＢＣＡ＜２×∠Ｒ、
  　∠ＢＣＡ＋∠ＣＡＢ＜２×∠Ｒ、
  　∠ＣＡＢ＋∠ＡＢＣ＜２×∠Ｒ
  のことである。
• 命題1-17は推論用命題である。

  前提	作図	推論
  定義
  公準	1-2
  公理		1-4、1-8補2
  命題		1-16
  その他

前 　　 次 　　 目次 　　頁頭