ユークリッド原論をどう読むか(4)
頁末
前
次
目次
ユークリッド原論
第1巻
命題1−48(三平方の定理の逆)
(正方形の大等小と辺の大等小)
もし
三角形において
1辺の上の正方形が
三角形の残りの2辺の上の正方形の和に
等しければ、
三角形の残りの2辺によって
はさまれる角は直角である。
三角形ABCにおいて
1辺BC上の正方形が
辺BA、AC上の正方形の和に
等しいとせよ。
角BACは直角であると主張する。
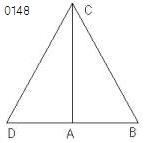
点Aから
線分ACに直角に
ADがひかれ、
ADがBAに等しくされ、
【・・・(a)】
DCが結ばれたとせよ。
DAは
ABに等しいから、
DA上の正方形もAB上の正方形に等しい。
双方に
AC上の正方形が加えられたとせよ。
そうすれば
DA、AC上の正方形の和は
BA、AC上の正方形の和に等しい。
ところが
角DACは直角であるから、
DC上の正方形は
DA、AC上の正方形の和に等しい。
【・・・(1)】
そして
仮定により
BC上の正方形は
BA、AC上の正方形の和に等しい。
ゆえに
DC上の正方形は
BC上の正方形に等しい。
したがって辺DCもBCに等しい。
- (a)
(1)
,定義1−22による。
- 正方形は、
面積が大きければ、
辺も大きい。
面積が等しければ
辺も等しい
(以下、命題1−48の補足(正方形の大等小と辺の大等小)という。)
これについては、
次のように証明される。
一方の面積が他方より大きいとする。
二つの正方形を、
一つの直角が重なり合うようにおくと、
定義1ー22により
小さい方の辺の他端は
大きい方の辺の上にある。
すると
小さい方の正方形の辺は
大きい方の正方形の辺の部分となり、
公理1−8により、
小さい方の正方形の辺は大きい方の正方形の辺より小さい。
両方の面積が等しいとする。
仮に
一方の辺が他方より大きいとする。
補足の前半の証明と同様にすると、
二つの正方形は等しくないことがわかる。
ところが
等しいはずであったから
矛盾する。
よって
二つの正方形の辺は等しい。
そして
DAはABに等しく、
ACは共通であるから、
2辺DA、ACは
2辺BA、ACに等しい。
そして底辺DCは
底辺BCに等しい。
それゆえ
角DACは角BACに等しい。
ところが
角DACは直角である。
ゆえに
角BACも直角である。
よって
もし
三角形において
1辺の上の正方形が
三角形の残りの2辺の上の正方形の和に
等しければ、
三角形の残りの2辺によって
はさまれる角は直角である。
これが証明すべきことであった。
- 原論第一巻の最終命題である。
直角三角形であることと、
三平方の定理が成立することとが
同値である
ことが証明された。
解析幾何に発展する内容が、
まったくの図形的考察のみで
導き出されることに、
注目すべきであろう。
-
命題1−48の補足(正方形の大等小と辺の大等小)
| 前提 | 作図 | 推論 |
| 定義 |
|
1-22
|
| 公準 |
|
|
| 公理 |
|
1-8
|
| 命題 |
|
|
| その他 |
|
背理法
|
- 命題1-48は推論用命題である。
第1巻の最後まで来れて、
正直ホッとしている所である。
今は、
約束を果たせて
よかったと思っている。
さて、蛇足になるが、
既に本紙に発表した内容について、
webページにアップしてある。
http://euc-elements.matrix.jp/indexframe.html
にある。
実質3フレーム構造で、
左下が目次用、
左上が図や命題などの補助的参照用、
右が本文用
となっている。
目次の黄色い文字や
命題番号をクリックすると、
補助的参照用のフレームに表示される。
命題のタイトル部分をクリックすると
本文用フレームに表示される。
上記の姿勢で
原論を読み進めて行きやすいように
工夫してある。
既に書き終えている命題でも
後の命題との関係で
読み返してみて
気づくことがしばしばある。
その度に
ページを更新している。
例えば、
命題1−7について、
命題そのものの訳に
微妙な言い回しの違いを感じて、
英文のページも参考にして、
表現を変えてみたりした。
読者の皆さんも
挑戦して見られてはどうだろうか。
今回の連載で、
原論の楽しみ方を
少しばかりとも感じていただけたとしたら、
もう少し解説を続けてみることも
あるかもしれない。
ご意見を待つことにしよう。
前
次
目次
頁頭
