ユークリッド原論をどう読むか（５）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論

第２巻

命題２ー８（和の平方と差の平方との差）
もし
　線分が任意に２分されるならば、
　全体と一つの部分とにかこまれた矩形の４倍と
　残りの部分の上の正方形と
　の和は
　全体の線分と先の部分とを
　一直線とした線分上の
　正方形に等しい。

• 線分は、定義の補足（命題１ー１）による。
• かこまれたは、定義２ー１による。
• 矩形は、定義１ー２２による。
• 倍は、定義の補足（公理１ー５）による。
• 正方形は、定義１ー２２による。
• 直線は、定義１ー４による。
• 等しいは、公理１−７による。

線分ＡＢが
　点Ｃで任意に分けられたとせよ。

• 　線分ＡＢ、
  　点Ｃ[ＡＢ]
  をとっている。

ＡＢ、ＢＣにかこまれた矩形の４倍と
　ＡＣ上の正方形と
　の和は
　ＡＢ、ＢＣを一直線とした［線分］上の
　正方形に等しいと主張する。

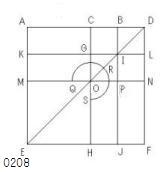
ＢＤがＡＢと一直線をなして延長され、

• 公準１ー２（作図.直線の延長）
  による。

ＢＤがＣＢに等しくされ、

• 延長された直線上に、
  　命題１ー３の補足（作図.等しい線分となる点）
  により
  　ＢからＣＢの長さに等しいところに
  　点Ｄをとる。
• 　点Ｄ(延長ＡＢ;;ＢＤ＝ＣＢ)
  をとっている。

ＡＤ上に正方形ＡＥＦＤが描かれ、

• 命題１ー４６（作図.線分上に正方形）
  による。
• 　正方ＡＥＦＤ(_ＡＤ)
  をとっている。

そして作図が二重に繰り返されたとせよ。

• 公準１ー１（作図.直線）
  により対角線ＤＥをひく。
  　命題１ー３１（作図・平行線）
  により
  　Ｂを通り
  　ＡＥに平行に直線をひく。
  　命題１ー３０の補足(交線に平行な線)
  により、
  　この直線はＤＥと交点Ｉをもち、
  　ＥＦと交点Ｊをもつ。
  命題１ー３１（作図・平行線）
  により
  　Ｉを通り
  　ＡＤに平行に直線をひく。
  命題１ー３０の補足(交線に平行な線)
  により、
  　この直線は
  　ＡＥと交点Ｋをもち、
  　ＤＦと交点Ｌをもつ。
  命題１ー３１（作図・平行線）
  により
  　Ｃを通り
  　ＡＥに平行に直線をひく。
  命題１ー３０の補足(交線に平行な線)
  により、
  　この直線は
  　ＫＬと交点Ｇをもち、
  　ＤＥと交点Ｏをもち、
  　ＥＦと交点Ｈをもつ。
  命題１ー３１（作図・平行線）
  により
  　Ｏを通り
  　ＡＤに平行に直線をひく。
  命題１ー３０の補足(交線に平行な線)
  により、
  　この直線は
  　ＡＥと交点Ｍをもち、
  　ＢＪと交点Ｐをもち、
  　ＤＦと交点Ｎをもつ。
• 原論の図は作図の順に交点の名前を付けていない。
• 　線分ＤＥ、
  　交点Ｉ(平行線(Ｂ,ＡＥ),ＤＥ)、
  　交点Ｊ(平行線(Ｂ,ＡＥ),ＥＦ)、
  　交点Ｋ(平行線(Ｉ,ＡＤ),ＡＥ)、
  　交点Ｌ(平行線(Ｉ,ＡＤ),ＤＦ)、
  　交点Ｇ(平行線(Ｃ,ＡＥ),ＫＬ)、
  　交点Ｏ(平行線(Ｃ,ＡＥ),ＤＥ)、
  　交点Ｈ(平行線(Ｃ,ＡＥ),ＥＦ)、
  　交点Ｍ(平行線(Ｏ,ＡＤ),ＡＥ)、
  　交点Ｐ(平行線(Ｏ,ＡＤ),ＢＪ)、
  　交点Ｎ(平行線(Ｏ,ＡＤ),ＤＦ)
  をとっている。

そうすれば
　ＣＢはＢＤに等しく、

• 作図の設定による。
• 　ＣＢ＝ＤＢ
  をとっている。

　他方ＣＢはＧＩに、
　ＢＤはＩＬに等しいから、

• 命題１ー３４（平行四辺形の対辺・対角・対角線）
  による。
• 　ＣＢ＝ＧＩ、
  　ＢＤ＝ＩＬ
  となっている。

ＧＩもＩＬに等しい。

• 公理１ー１（同じものに等しい）
  による。
• 　ＧＩ＝ＩＬ
  となっている。

同じ理由でＯＰもＰＮに等しい。
そしてＢＣはＢＤに、
　ＧＩはＩＬに等しいから、
　［矩形］ＣＩもＩＤに、ＧＰもＰＬに等しい。

• 命題１ー３６（平行四辺形の等積変形２）
  による。
• 　ＣＢ＝ＢＤ、
  　ＧＩ＝ＩＬ、
  　矩形(ＣＩ)＝矩形(ＩＤ)、
  　矩形(ＧＰ)＝矩形(ＰＬ)
  　　　　　　【・・・(1)】

ところが
　ＣＩはＰＬに等しい。
なぜなら
　平行四辺形ＣＭの補形であるから。

• 「なぜなら・・・であるから」については、
  　コメント２（命題１ー１６）を参照のこと。
• 命題１ー４３（平行四辺形の補形）
  による。
• 　矩形(ＣＩ)＝矩形(ＰＬ)
  　　　　　　【・・・(2)】

それゆえ
　ＩＤもＧＰに等しい。

• 公理１ー１の補足（等しいものに等しい）
  による。
• (1) (2) により
  　矩形(ＩＤ)＝矩形(ＧＰ)
  　　　　　　【・・・(3)】

ゆえに
　ＤＩ、ＣＩ、ＧＰ、ＰＬの四つは
　互いに等しい。

• (1) (2) (3) により
  　矩形(ＣＩ)＝矩形(ＩＤ)
  　＝矩形(ＧＰ)＝矩形(ＰＬ)
  　　　　　　【・・・(4)】

したがって
　この四つの和はＣＩの４倍である。

• 定義の補足（公理１ー５）（同じもののｎ倍）
  による。
• (4) により
  　　矩形(ＣＩ)＝矩形(ＩＤ)
  　＝矩形(ＧＰ)＝矩形(ＰＬ)
  　＝４×矩形(ＣＩ)
  　　　　　　【・・・(5)】

また
　ＣＢはＢＤに等しく、

• 作図の設定による。
• 　ＣＢ＝ＢＤ
  となっている。

他方ＢＤはＢＩすなわちＣＧ等しく、
　ＣＢはＧＩすなわちＧＯに等しいから、

• 命題２ー４の補足(正方形の対角線をはさむ正方形)
  と命題１ー３４（平行四辺形の対辺・対角・対角線）
  とによる。
• 　ＢＤ＝ＢＩ＝ＣＧ、
  　ＣＢ＝ＧＩ＝ＧＯ
  となっている。

ＣＧもＧＯに等しい。

• 公理１ー１（同じものに等しい）
  による。
• 　ＣＧ＝ＧＯ
  となっている。

そして
　ＣＧはＧＯに、
　ＯＰはＰＮに等しいから

• 先に証明されている。
• 　ＣＧ＝ＧＯ、
  　ＯＰ＝ＰＮ
  となっている。

［矩形］ＡＧもＫＯに、ＯＪもＰＦに等しい。

• 命題１ー３４（平行四辺形の対辺・対角・対角線）
  により、
  　ＡＣとＫＧとが等しく、
  　ＰＪとＮＦとが等しいので、
  　定義２ー１（かこまれる）
  による。
• 　矩形(ＡＧ)＝矩形(ＫＯ)、矩形(ＯＪ)＝矩形(ＰＦ)
  　　　　　　【・・・(6)】

ところが
　ＫＯはＯＪに等しい。
なぜなら
　平行四辺形ＫＪの補形であるから。

• 「なぜなら・・・であるから」については、
  　コメント２（命題１ー１６）を参照のこと。
• 命題１ー４３（平行四辺形の補形）
  による。
• 　矩形(ＫＯ)＝矩形(ＯＪ)
  　　　　　　【・・・(7)】

それゆえ
　ＡＧもＰＦに等しい。

• 公理１ー１の補足（等しいものに等しい）
  による。
• (6) (7) により
  　矩形(ＡＧ)＝矩形(ＰＦ)
  　　　　　　【・・・(8)】

ゆえに
　ＡＧ、ＫＯ、ＯＪ、ＰＦの四つは
　互いに等しい。

• (6) (7) (8) により
  　矩形(ＡＧ)＝矩形(ＫＯ)
  　＝矩形(ＯＪ)＝矩形(ＰＦ)
  　　　　　　【・・・(9)】

したがって
　この四つの和はＡＧの４倍である。

• 定義の補足（公理１ー５）（同じもののｎ倍）
  による。
• (9) により
  　矩形(ＡＧ)＝矩形(ＫＯ)
  　＝矩形(ＯＪ)＝矩形(ＰＦ)
  　＝４×矩形(ＡＧ) 　　　　　　【・・・(10)】

しかも
　ＣＩ、ＩＤ、ＧＰ、ＰＬ四つの和が
　ＣＩの４倍であることも先に証明された。

• (5) による。
• 　矩形(ＣＩ)＝矩形(ＩＤ)
  　＝矩形(ＧＰ)＝矩形(ＰＬ)
  　＝４×矩形(ＣＩ)
  となっている。

それゆえ
　グノーモーンＱＲＳを構成する八つの和は
　ＡＩの４倍である。

• 公理１ー７（等しい）、
  　公理１ー２（等しいものに等しいものを加える）
  による。
• (5) (10) により
  　グ(ＱＲＳ)＝４×矩形(ＡＩ)
  　　　　　　【・・・(11)】

そして
　ＢＩがＢＤに等しいため、

• 作図の設定による。
• 　ＢＩ＝ＢＤ
  となっている。

　ＡＩは
　矩形ＡＢ、ＢＤに等しいから、

• 定義２−１（かこまれる）
  による。
• 　矩形(ＡＩ)＝矩形(ＡＢ、ＢＤ)
  　　　　　　【・・・(12)】

　矩形ＡＢ、ＢＤの４倍は
　ＡＩの４倍である。

• 公理１ー５（同じものの２倍） 、
  　定義の補足（公理１ー５）（同じもののｎ倍）
  による。
• (12) により　
  　４×矩形(ＡＩ)＝４×矩形(ＡＢ、ＢＤ)
  　　　　　　【・・・(13)】

また
　グノーモーンＱＲＳも
　ＡＩの４倍であることが
　先に証明された。
それゆえ
　矩形ＡＢ、ＢＤの４倍は
　グノーモーンＱＲＳに等しい。

• 公理１ー１（同じものに等しい）
  による。
• (11) (13) により
  　グ(ＱＲＳ)＝４×矩形(ＡＩ)
  よって
  　グ(ＱＲＳ)＝４×矩形(ＡＢ、ＢＤ)
  　　　　　　【・・・(14)】

双方に
　ＡＣ上の正方形に等しいＭＨが
　加えられたとせよ。

• 命題２ー４の補足(正方形の対角線をはさむ正方形)
  による。
• 　矩形(ＭＨ)＝正方(_ＡＣ)
  　　　　　　【・・・(15)】

そうすれば
　ＡＢ、ＢＤにかこまれた矩形の４倍と
　ＡＣ上の正方形と
　の和は
　グノーモーンＱＲＳとＭＨと
　の和に等しい。

• 公理１ー２（等しいものに等しいものを加える）
  による。
• (14) (15) により
  　グ(ＱＲＳ)＋矩形(ＭＨ)
  　＝４×矩形(ＡＢ、ＢＤ)＋正方(_ＡＣ)
  　　　　　　【・・・(16)】

ところが
　グノーモーンＱＲＳとＭＨと
　の和は
　ＡＤ上の正方形ＡＥＦＤに等しい。

• 公理１ー７（等しい）
  による。
• 　グ(ＱＲＳ)＋矩形(ＭＨ)
  　＝正方(_ＡＤ)
  　　　　　　【・・・(17)】

しかも
　ＢＤはＢＣに等しい。

• 作図の設定である。
• したがって
  　矩形(ＡＢ、ＢＤ)＝矩形(ＡＢ、ＢＣ)
  　　　　　　【・・・(18)】

それゆえ
　ＡＢ、ＢＣにかこまれた矩形の４倍と
　ＡＣ上の正方形と
　の和は
　ＡＤ上の正方形、
　すなわち
　ＡＢ、ＢＣを一直線とした上の正方形に等しい。

• 公理１ー１（同じものに等しい）、
  　公理１ー２（等しいものに等しいものを加える）
  による。
• (16) (17) (18) により
  　４×矩形(ＡＢ、ＢＤ)＋正方(_ＡＣ)＝正方(_ＡＤ)
  したがって
  　４×矩形(ＡＢ、ＢＣ)＋正方(_ＡＣ)＝正方(_ＡＤ)
  

よってもし
　線分が
　任意に２分されるならば、
　全体と一つの部分とにかこまれた矩形の４倍と
　残りの部分の上の正方形と
　の和は
　全体の線分と先の部分とを一直線とした
　線分上の正方形に等しい。
　
これが証明すべきことであった。

• 以下の証明が可能である。
  矩形ＡＢ、ＢＣの２倍とＣＡ上の正方形と
  　の和は
  　命題２ー７（差の平方）
  により
  　ＡＢ上の正方形とＢＣ上の正方形と
  　の和に等しい。
  
  • 　２×矩形(ＡＢ、ＢＣ)＋正方(_ＣＡ)
    　＝正方(_ＡＢ)＋正方(_ＢＣ)
    　　　　　　【・・・(19)】
  ＢＣは
  命題の設定により
  　ＢＤに等しいから、
  　ＢＣ上の正方形は
  　定義１ー２２（正方形・矩形・菱形・長斜方形・トラペジオン）
  により
  　ＢＤ上の正方形に等しい。
  
  • 　正方(_ＢＣ)＝正方(_ＢＤ)
    　　　　　　【・・・(20)】
  また
  　矩形ＡＢ、ＢＣは
  　定義２ー１（かこまれる）
  により
  　矩形ＡＢ、ＢＤに等しい。
  
  • 　矩形(ＡＢ、ＢＣ)＝矩形(ＡＢ、ＢＤ)
    　　　　　　【・・・(21)】
  ＡＢ上の正方形とＢＣ上の正方形と
  　の和は
  　公理１ー２（等しいものに等しいものを加える）
  により
  　ＡＢ上の正方形とＢＤ上の正方形と
  　の和に等しく、
  
  • (20) により
    　正方(_ＡＢ)＋正方(_ＢＣ)＝正方(_ＡＢ)＋正方(_ＢＤ)
    　　　　　　【・・・(22)】
  　矩形ＡＢ、ＢＣの２倍とＣＡ上の正方形と
  　の和は
  　矩形ＡＢ、ＢＤの２倍とＣＡ上の正方形と
  　の和は等しいから、
  
  • (21) により
    　２×矩形(ＡＢ、ＢＣ)＋正方(_ＣＡ)
    　＝２×矩形(ＡＢ、ＢＤ)＋正方(_ＣＡ)
    　　　　　　【・・・(23)】
  　矩形ＡＢ、ＢＤの２倍とＣＡ上の正方形と
  　の和は
  　公理１ー１の補足（等しいものに等しい）
  により
  　ＡＢ上の正方形とＢＤ上の正方形と
  　の和に等しい。
  
  • (19) (22) (23) により
    　２×矩形(ＡＢ、ＢＤ)＋正方(_ＣＡ)
    　＝正方(_ＡＢ)＋正方(_ＢＤ)
    　　　　　　【・・・(24)】
  双方に
  　矩形ＡＢ、ＢＤの２倍が加えられたとせよ。
  矩形ＡＢ、ＢＤの４倍とＣＡ上の正方形は、
  　公理１ー２（等しいものに等しいものを加える）
  により
  　矩形ＡＢ、ＢＤの２倍と
  　ＡＢ上の正方形とＢＤ上の正方形と
  　の和に等しい。
  
  • (24) により
    　２×矩形(ＡＢ、ＢＤ)＋正方(_ＣＡ)
    　＋２×矩形(ＡＢ、ＢＤ)
    　＝正方(_ＡＢ)＋正方(_ＢＤ)
    　＋２×矩形(ＡＢ、ＢＤ)
    となるので、
    　４×矩形(ＡＢ、ＢＤ)＋正方(_ＣＡ)
    　＝２×矩形(ＡＢ、ＢＤ)
    　＋正方(_ＡＢ)＋正方(_ＢＤ)
    　　　　　　【・・・(25)】
  ＡＢ上の正方形とＢＤ上の正方形と
  　矩形ＡＢ、ＢＤの２倍と
  　の和は
  　命題２ー４（２分線分上の正方形）
  により
  　ＡＤ上の正方形に等しい。
  
  • 　２×矩形(ＡＢ、ＢＤ)
    　＋正方(_ＡＢ)＋正方(_ＢＤ)
    　＝正方(_ＡＤ)
    　　　　　　【・・・(26)】
  よって、
  　矩形ＡＢ、ＢＤの４倍とＣＡ上の正方形と
  　の和は
  公理１ー１（同じものに等しい）
  により
  　ＡＤ上の正方形に等しい。
  
  • (25) (26) により
    　４×矩形(ＡＢ、ＢＤ)＋正方(_ＣＡ)
    　＝正方(_ＡＤ)
    　　　　　　【・・・(27)】
  ところが
  　矩形ＡＢ、ＢＤは
  　定義２ー１（かこまれる）
  により
  　矩形ＡＢ、ＢＣに等しい。
  
  • 　矩形(ＡＢ、ＢＤ)＝矩形(ＡＢ、ＢＣ)
    　　　　　　【・・・(28)】
  したがって、
  　公理１ー２（等しいものに等しいものを加える）、
  　公理１ー１（同じものに等しい）
  により
  　矩形ＡＢ、ＢＣの４倍とＣＡ上の正方形と
  　の和はＡＤ上の正方形に等しい。
  • (27) (28) により
    　４×矩形(ＡＢ、ＢＣ)＋正方(_ＣＡ)
    　＝正方(_ＡＤ)
    　　　　　　【・・・(29)】
  • 命題2-8は第２巻の命題によると次のようになる。

    前提	作図	推論
    定義		1-22,2-1
    公準
    公理		1-1,1-1補,1-2
    命題		2-4,2-7
    その他

• 本質的には、和の平方と差の平方との差のことである。
  　４×ＢＣ＋正方(_ＡＢーＢＣ)
  　＝正方(_ＡＢ＋ＢＣ)
  　となるが、
  　正方(_ＡＢーＢＣ)
  　を移項して
  　４×ＢＣ＝正方(_ＡＢ＋ＢＣ)ー正方(_ＡＢーＢＣ)
  　となる。
  　
• 命題2-8は、
  　ＡＢ；線分
  に対して、
  　Ｃ；点（ＡＢ）、
  　Ｄ；点（ＡＢの延長上、ＢＤ＝ＢＣ）
  をとれば
  　４×矩形(ＡＢ、ＢＣ)＋正方(_ＡＢーＢＣ)
  　＝正方(_ＡＢ＋ＢＣ)
  のことである。
• 命題2-8は推論用命題である。

  前提	作図	推論
  定義		補(理1-5),2-1
  公準	1-1,1-2
  公理		1-1,1-1補,1-2,1-7
  命題	1-3補,1-30補,1-31,1-46	1-30,1-34,1-36,1-43,2-4補
  その他		コ2(題1-16)f

  　

前 　　 次 　　 目次 　　頁頭