ユークリッド原論をどう読むか(4)
頁末
前
次
目次
ユークリッド原論
第1巻
命題1−43(平行四辺形の補形)
対角線をはさむ平行四辺形・補形
(作図.対角線をはさむ平行四辺形)
すべての平行四辺形において
対角線をはさむ
二つの平行四辺形の補形は
互いに等しい。
- 平行四辺形は、定義の補足(命題1−34)による。
- 対角線は、定義の補足(命題1−34)による。
- 対角線をはさむ平行四辺形とは、
対角線の一端と対角線上の1点とを
向かい合う頂点とし
元の平行四辺形の辺と平行な辺でできる
二つの平行四辺形をいう。
これらの平行四辺形は
元の対角線の一部を
対角線としてもつ。
この補形とは
平行四辺形から
これら、対角線をはさむ二つの平行四辺形を
除いて残る
二つの平行四辺形をいう。
(以下、定義の補足(命題1−43)(対角線をはさむ平行四辺形・補形)という。)
命題1−44作図.線分,三角形,直線角と平行四辺形)
も参照すること。
- 等しいは、公理1−7による。
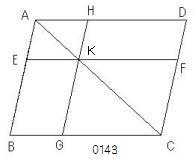
ABCDを平行四辺形、
ACをその対角線とし、
EH、FGを
ACはさむ平行四辺形、
BK、KDを
いわゆる補形とせよ。
-
作図.対角線をはさむ平行四辺形(以下、命題1ー43の補足2(作図.対角線をはさむ平行四辺形)という。)
は、
次による。
公準1ー1の補足(作図.任意の点をとる)
により、
AB上に点Eをとる。
命題1ー31(作図・平行線)
により、
Eを通り
辺ADに平行に直線をひくと、
この直線は、
命題1ー30の補足(交線に平行な線)
により
ADがACと交わっているので、
ACと交わり、
その交点をKとする。
また、
この直線は、
ABがDCと平行であるので、
命題1ー30の補足(交線に平行な線)
により
DCと交わり、
その交点をFとする。
次に
命題1ー31(作図・平行線)
により、
Kを通り
辺ABに平行に直線をひくと、
この直線は、
ACがBCと交わっているので、
命題1ー30の補足(交線に平行な線)
により
BCと交わり、
その交点をGとする。
また、
この直線は、
ACがADと交わっているので、
命題1ー30の補足(交線に平行な線)
により
ADと交わり、
その交点をHとする。
-
平行四辺形ABCD
に対して、
点E[AB]、
交点K(AC,平行線(E,AD))、
交点F(DC,平行線(E,AD))、
交点G(BC,平行線(K,AB))、
交点H(AD,平行線(K,AB))、
をとっている。
補形BKは補形KDに等しい
と主張する。
ABCDは平行四辺形であり、
ACはその対角線であるから、
三角形ABCは三角形ACDに等しい。
【・・・(1)】
- 命題1−34(平行四辺形の対辺・対角・対角線)
による。
-
△ABC=△ACD
となっている。
また
EHは平行四辺形であり、
AKはその対角線であるから、
三角形AEKは三角形AHKに等しい。
同じ理由で
三角形KFCもKGCに等しい。
そこで
三角形AEKは三角形AHKに、
KFCはKGCに
等しいから、
三角形AEKとKGCの和は
三角形AHKとKFCの和に等しい。
- 公理1−2(等しいものに等しいものを加える)
による。
-
△AEK+△KGC=△AHK+△KFC
となっている。
しかも
三角形ABC全体は
三角形ADC全体に等しい。
- (1)
命題1−34(平行四辺形の対辺・対角・対角線)
による。
-
△ABC=△ADC
となっている。
それゆえ
残りの補形BKは
残りの補形KDに等しい。
- 公理1−3(等しいものから等しいものをひく)
による。
-
平四(BK)=平四(KD)
となっている。
よって
すべての平行四辺形において
対角線をはさむ
二つの平行四辺形の補形は
互いに等しい。
これが証明すべきことであった。
- この命題では、
平行四辺形を
向かい合う頂点1組だけで
表現している。
- この命題が、
直線図形を
指定された角におさまる
平行四辺形に
等積変形する第二歩のための準備である。
- 命題1-43は、
平行四辺形ABCD
に対して、
点E[AB]、
交点K(AC,平行線(E,AD))、
交点F(DC,平行線(E,AD))、
交点G(BC,平行線(K,AB))、
交点H(AD,平行線(K,AB))、
をとれば、
平四(BK)=平四(KD)
のことである。
-
命題1ー43の補足2(作図.対角線をはさむ平行四辺形)
- 命題1-43は推論用命題である。
前
次
目次
頁頭
