ユークリッド原論をどう読むか（４）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー３６（平行四辺形の等積変形２）
等しい底辺の上にあり
　かつ
　同じ平行線の間にある
　平行四辺形は
　互いに等しい。

• 等しいは、公理１ー７による。
• 底辺は、定義の補足（命題１ー３５）による。
• 平行線は、定義１ー２３による。
• 平行四辺形は、定義の補足（命題１ー３４）による。
• 等しいは、公理１ー７による。

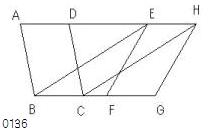
ＡＢＣＤ、ＥＦＧＨを
　等しい底辺ＢＣ、ＦＧの上にあり
　かつ
　同じ平行線ＡＨ、ＢＧの間にある
　平行四辺形とせよ。

• 　線分ＢＧ
  に対して、
  　点Ｃ[ＢＧ]、
  　点Ｆ(ＢＧ;;ＦＧ＝ＢＣ)、
  　点Ａ[外.ＢＧ]、
  　平行線ＡＨ[Ａ,ＢＧ]、
  　点Ｄ(ＡＨ;;ＡＤ＝ＢＣ)、
  　点Ｅ(ＡＨ;;ＥＨ＝ＦＧ)、
  　平行四辺形ＡＢＣＤ、
  　平行四辺形ＥＦＧＨ
  をとっている。
  

平行四辺形ＡＢＣＤは
　ＥＦＧＨに等しいと主張する。


ＢＥ、ＣＨが結ばれたとせよ。

• 公準１ー１（作図.直線）
  による。
• 　線分ＢＥ、ＣＨ
  をとっている。

そうすれば
　ＢＣはＦＧに等しく、

• 命題の設定 による。
• 　ＢＣ＝ＦＧ
  となっている。

また
　ＦＧはＥＨに等しいから、

• 命題１ー３４（平行四辺形の対辺・対角・対角線）
  による。
• 　ＦＧ＝ＥＨ
  となっている。

ＢＣもＥＨに等しい。

• 公理１ー１（同じものに等しい）
  による。
• 　ＢＣ＝ＥＨ
  となっている。

しかも
　平行である。

• 命題の設定 による。
• 　ＢＣ‖ＥＨ
  となっている。

そして
　ＥＢ、ＨＣがそれらを結んでいる。
ところが
　等しくかつ平行な線分を
　同じ側で結ぶ２線分は
　等しくかつ平行である。

• 命題１ー３３（等しく平行な２線分）
  である。

それゆえ
　ＥＢＣＨは平行四辺形である。

• 定義の補足（命題１ー３４）(平行四辺形・対角線)
  による。
• 　ＥＢＣＨ;平行四辺形
  となっている。

そして
　ＡＢＣＤに等しい。
　　　　　　【・・・(1)】
なぜなら
　それと同じ底辺ＢＣをもち、
　それと同じ平行線ＢＣ、ＡＨの間に
　あるからである。

• 「なぜなら・・・であるから」については、
  　コメント２（命題１ー１６）を参照のこと。
• 命題１ー３５（平行四辺形の等積変形１）
  による。
• 　平行四辺形ＥＢＣＨ＝平行四辺形ＡＢＣＤ
  となっている。

同じ理由で
　ＥＦＧＨも同じＥＢＣＨに等しい。

• 　平行四辺形ＥＦＧＨ＝平行四辺形ＥＢＣＨ
  となっている。

したがって
　平行四辺形ＡＢＣＤもＥＦＧＨに等しい。

• (1) ,公理１ー１（同じものに等しい）
  による。
• 　平行四辺形ＡＢＣＤ＝平行四辺形ＥＦＧＨ
  となっている。

よって
　等しい底辺の上にあり
　かつ同じ平行線の間にある
　平行四辺形は互いに等しい。
　
これが証明すべきことであった。

• 命題１ー３５は、
  　同一の底辺を持つ平行四辺形についてであったが、
  　本命題は、
  　同じ平行線上に
  　長さが等しい底辺をもつ場合について論じている。
  この場合、
  　２つの平行四辺形の重なり具合が
  　いろいろあるが、
  　本論のように、
  　全く重ならない場合について証明すれば、
  　重なっている場合でも、
  　双方ともに重ならない位置に
  　等しい底辺を持つ等しい平行四辺形を
  　考えることにより
  　論証できる。
• 命題1-36は、
  　線分ＢＧ
  に対して、
  　点Ｃ[ＢＧ]、
  　点Ｆ(ＢＧ;;ＦＧ＝ＢＣ)、
  　点Ａ[外.ＢＧ]、
  　平行線ＡＨ[Ａ,ＢＧ]、
  　点Ｄ(ＡＨ;;ＡＤ＝ＢＣ)、
  　点Ｅ(ＡＨ;;ＥＨ＝ＦＧ)、
  　平行四辺形ＡＢＣＤ、
  　平行四辺形ＥＦＧＨ
  をとるならば、
  　平行四辺形ＡＢＣＤ＝平行四辺形ＥＦＧＨ
  のことである。
  
• 命題1-36は推論用命題である。

  前提	作図	推論
  定義		補（題1-34）
  公準	1-1
  公理		1-1
  命題		1-33、1-34、1-35
  その他		コ2(題1-16)f

前 　　 次 　　 目次 　　 頁頭