ユークリッド原論をどう読むか(14)
頁末
前
次
目次
ユークリッド原論
第10巻
命題10ー74(中項線分から平方のみ通約で有理面積をかこむ中項線分を引くと第1の中項余線分)
第1の中項余線分
もし
中項線分から
全体と
平方においてのみ通約
でき、
全体とともに有理面積を
かこむ
中項線分が
ひかれる
ならば、
残りは
無理線分である。
そして
第1の中項余線分
とよぱれる。
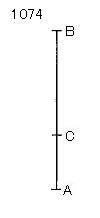
中項線分ABから
中項線分BCが
ひかれ、
BCは
ABと平方においてのみ通約
でき、
ABと共に
有理面積である矩形AB、BCを
つくる
とせよ。
-
命題10ー27(作図.2中項線分;矩形が有理面積、平方でのみ通約)
により、
2中項線分を
とり、
大きい方を
AB、
小さい方を
BC
とする。
命題1ー3(作図・等しい線分を切り取る)
により、
C’(AB;BC’=BC)をとり、
改めて、
C’を
C
とする。
-
AB、BC;中項線分、
AB∩^^2 BC
矩形(AB、BC);有理面積
となっている。
残りのACは
無理線分
である
と主張する。
そして
第1の中項余線分
とよばれる。
AB、BCは
中項線分
である
から、
AB、BC上の正方形の和も
中項面積
である。
ところが
矩形AB、BCの2倍は
有理面積
である。
したがって
AB、BC上の正方形の和は
矩形AB、BCの2倍と
通約できない。
-
前節、前々節、
命題10ー23の補足6(有理面積と中項面積は非通約)
による。
-
正方(_AB)+正方(_BC)¬∩2矩形(AB、BC)
となっている。
それゆえ
矩形AB、BCの2倍は
残りのAC上の正方形と
通約できない。
なぜなら
もし
二つの量が
加えられた
とき、
全体が
それらの一方と
通約できな
ければ、
最初の2量も
相互に
通約できないであろう
から。
-
前節、
命題2ー7(差の平方)
による。
-
「なぜなら・・・であるから(for)」と
簡潔な論拠を後から示している。
後世の解説者のコメントが
混入したものと思われる。
コメント2(命題1ー16)、
コメント(命題1ー4)
を参照のこと。
-
2矩形(AB、BC)¬∩正方(_AC)
となっている。
ところが
矩形AB、BCの2倍は
有理面積
である。
-
命題の設定による。
-
2矩形(AB、BC);有理面積
となっている。
したがって
AC上の正方形は
無理面積
である。
-
前節、
定義10ー4の補足(有理面積、無理面積)
による。
-
正方(_AC);無理面積
となっている。
よって
ACは
無理線分
である。
-
前節、
定義10ー4(面積の有理、無理、無理線分)
による。
-
AC;無理線分
となっている。
そして
第1の中項余線分
とよぱれる。
- 命題10ー74は、
命題10ー27(作図.2中項線分;矩形が有理面積、平方でのみ通約)
により、
2中項線分を
とり、
大きい方を
AB、
小さい方を
BC
命題1ー3(作図・等しい線分を切り取る)
により、
ACからBCを引くと、
ACは
第1の中項余線分
とよばれる
無理線分
のことである。
- 命題10ー74は推論用命題である。
前
次
目次
頁頭
