ユークリッド原論をどう読むか（１４）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第１０巻
　
命題１０ー４６（中項面積と有理面積の和に等しい正方形の辺の分割は１通り）
　中項面積と有理面積の和
　に等しい正方形の辺は
　　ただ一つの点で分けられる。

• 中項面積と有理面積の和に等しい正方形の辺は、
  定義の補足（命題１０ー４０） による。
• 点は、
  定義１ー１による。

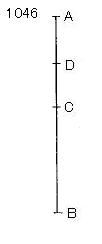
　ＡＢをＣで分けられる
　中項面積と有理面積の和
　に等しい正方形の辺
とし，したがって
　ＡＣ，ＣＢが平方において通約できず，
　ＡＣ，ＣＢ上の正方形の和を中項面積とし，
　矩形ＡＣ，ＣＢの２倍を有理面積とする
とせよ。

• 　命題１０ー３４（作図.２線分；平方で非通約、平方和が中項面積、矩形が有理面積）
  により、
  　線分ＡＣ、ＣＢ
  　　；ＡＣ¬∩^^2 ＣＢ
  　　　、正方(_ＡＣ)＋正方(_ＣＢ)；中項面積
  　　　、矩形(ＡＣ,ＣＢ)；有理面積
  　線分ＡＢ；ＡＣ＋ＣＢ
  をとれば、
  　命題１０ー４０（平方で非通約、平方和が中項面積、かこむ矩形が有理面積の２線分の和は、中項と有理面積の和となる正方形の辺）
  による。
  
• 　線分ＡＣ；中項面積と有理面積の和に等しい正方形の辺
  となっている。

　ＡＢは
　　他の点で分けられない
と主張する。

もし可能ならば，

• 　背理法の仮定を述べようとしている。

　Ｄでも分けられるとし，
　ＡＤ，ＤＢが平方において通約できず，
　ＡＤ，ＤＢ上の正方形の和を中項面積とし，
　矩形ＡＤ，ＤＢの２倍を有理面積とする

• 　コメント(命題１０ー４２助)(点対称点の除外)
  による。
  　ただし、
  　この命題においては、
  　ＡＣ＜ＢＤ
  　とされている。
• 　線分ＡＤ、ＤＢ
  　　；ＡＤ¬∩^^2 ＤＢ
  　　　、正方(_ＡＤ)＋正方(_ＤＢ)；中項面積
  　　　、矩形(ＡＤ,ＤＢ)；有理面積
  　ＡＣ＜ＢＤ
  としている。

とせよ。そうすれば
　矩形ＡＣ，ＣＢの２倍と
　　矩形ＡＤ，ＤＢの２倍との差は
　ＡＤ，ＤＢ上の正方形の和と
　　ＡＣ，ＣＢ上の正方形の和との差に等しく，

• 　命題２ー４（２分線分上の正方形）、
  　公理１ー３（等しいものから等しいものをひく）
  による。
• 　正方(_ＡＣ)＋正方(_ＣＢ)
  　　ー｛正方(_ＡＤ)＋正方(_ＤＢ)｝
  　　　＝２矩形(ＡＤ,ＤＢ)ー２矩形(ＡＣ,ＣＢ)
  となっている
  

　矩形ＡＣ，ＣＢの２倍が
　　矩形ＡＤ，ＤＢの２倍より有理面積だけ大きい

• 　命題の設定、
  　定義１０ー４の補足（有理面積、無理面積）
  　命題１０ー１５（通約量はその和・差とも通約）
  による。
  
• 　２矩形(ＡＣ,ＣＢ)ー２矩形(ＡＤ,ＤＢ)；有理面積
  となっている。

から，
　ＡＤ，ＤＢ上の正方形の和は
　　ＡＣ，ＣＢ上の正方形の和より，
　　共に中項面積である
のに，
　　有理面積だけ大きい。

• 　命題の設定、
  　前節、前々節、
  　命題１０ー２６（中項面積の差は無理面積）
  による。
  
• 　正方(_ＡＣ)＋正方(_ＣＢ)
  　　ー｛正方(_ＡＤ)＋正方(_ＤＢ)｝；無理面積
  　＝２矩形(ＡＤ,ＤＢ)ー２矩形(ＡＣ,ＣＢ)　；有理面積
  となっている。

これは不可能である。
したがって
　中項面積と有理面積の和
　に等しい正方形の辺は
　　異なる２点で分けられない。

• 　背理法による。
• 　中項面積と有理面積の和
  　に等しい正方形の辺の分割点は
  　　ただ一つ
  となっている。 　

よって
　一つの点で分けられる。
これが証明すべきことであった。

• 命題１０ー４６は、
  　線分ＡＣ、ＣＢ
  　　；ＡＣ¬∩^^2 ＣＢ
  　　　、正方(_ＡＣ)＋正方(_ＣＢ)；中項面積
  　　　、矩形(ＡＣ,ＣＢ)；有理面積
  　線分ＡＢ；ＡＣ＋ＣＢ
  　　、中項面積と有理面積の和に等しい正方形の辺
  をとれば、
  　本質的に分割点はＣのみ
  のことである
• 命題１０ー４６は推論用命題である。

  前提	作図・構成	推論
  定義		10-4補
  公準
  公理		1-3
  命題	10-34	2-4,10-15,10-26,10-40
  その他		コ(題10-42助),背理法

前 　　 次 　　 目次 　　頁頭