ユークリッド原論をどう読むか（１４）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第１０巻
　
命題１０ー２４（長さで通約の中項線分の矩形は中項面積）

　長さにおいて通約できる
　中項線分によって
　かこまれる矩形は
　中項面積である。

• 長さにおいて通約は、
  定義１０ー２の補足による。
• 中項線分は、
  定義の補足（命題１０ー２１）による。
• かこまれるは、
  定義２ー１による。
• 矩形は、
  定義１ー２２による。
• 中項面積は、
  定義の補足２（命題１０ー２３）による。

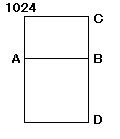
　矩形ＡＣが
　長さにおいて通約できる
　中項線分ＡＢ、ＢＣによって
　かこまれた
とせよ。

• 　命題１０ー２２の補足(作図.中項線分)
  により、
  　中項線分ＡＢをひき、
  　命題１０ー６の系３（作図.長さ・平方で通約可の線分)
  により、
  　ＡＢと通約できる線分ＢＣをひくと、
  　命題１０ー２３（中項線分と平方で通約なら中項線分）
  により
  　ＢＣは中項線分になる。
  　命題２ー１の補足（作図.矩形）
  により、
  　矩形ＡＢ、ＢＣをつくる。
  
• 　ＡＢ∩ＢＣ、
  　ＡＢ、ＢＣ；中項線分、
  　rec(ＡＣ)＝rec(ＡＢ、ＢＣ)
  となっている。
  

　ＡＣは中項面積である
と主張する。

　ＡＢ上に
　正方形ＡＤが描かれた
とせよ。
　　　　　　[......(ａ)]

• 　命題１−４６（作図.線分上に正方形）
  による。
  

そうすれば
　ＡＤは中項面積である。
　　　　　　[......(１)]

• 　前節、
  　定義の補足２（命題１０ー２３）(中項面積)
  による。
• 　ＡＤ；中項面積
  となっている。

そして
　ＡＢは
　ＢＣと長さにおいて通約でき、

• 　命題の設定による。
• 　ＡＢ∩ＢＣ
  となっている。
  

　ＡＢはＢＤに等しい

• 　（ａ）
  　定義１ー２２（正方形・矩形・菱形・長斜方形・トラペジオン）
  による。
  

から、
　ＤＢも
　ＢＣと長さにおいて通約できる。

• 　前節、
  　定義１０ー１（通約）
  により
  　ＢＤはＡＢと通約でき、
  　これと、
  　前々節、
  　命題１０ー１２（通約量と通約なら通約）
  による。
• 　ＤＢ∩ＢＣ
  となっている。

したがって
　ＤＡもＡＣと通約できる。

• 　命題６ー１（同高の三角形、平行四辺形は底辺と比例）
  により
  　sq(ＤＡ)：rec(ＡＣ)＝ＤＢ：ＢＣ
  となっており、
  　前節、
  　命題１０ー１２（通約量と通約なら通約）
  による。
  
• 　ＤＡ∩ＡＣ
  となっている。

そして
　ＤＡは中項面積である。

• 　（１）による。
• 　sq(ＤＡ)；中項面積
  となっている。

ゆえに
　ＡＣも中項面積である。

• 　前節、前々節
  　命題１０ー２３の系 (中項面積と通約なら中項面積)
  による。
• 　rec(ＡＣ)；中項面積
  となっている。

　これが証明すべきことであった。

• 命題１０ー２４は、
  　Ａ、Ｂ：中項線分、
  　Ａ∩Ｂ
  ならば、
  　rec(Ａ、Ｂ)：中項面積
  のことである。
• 命題１０ー２４は推論用命題である。

  前提	作図・構成	推論
  定義		1-22,10-1,補2(命題10-23)
  公準
  公理
  命題	1-46,2-1補,10-6系3,10-22補	6-1,10-12,10-23,10-23系
  その他

前 　　 次 　　 目次 　　頁頭