ユークリッド原論をどう読むか（１４）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第１０巻
　
命題１０ー１２（通約量と通約なら通約）

　同一の量と通約できる量は
　相互にも通約できる。

• 量は、
  定義５ー１の補足による。
• 通約は、
  定義１０ー１による。

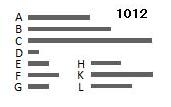
　Ａ、Ｂの双方がＣと通約できる
とせよ。

• 　「量（について）・・・とせよ」は、
  　コメント６（命題５ー１）
  　参照のこと。
  
• 　量を線分で表現する
  とすれば、
  　作図は次のようになる。
  
  　公準１ー１の補足２（作図.任意の線分）
  により
  　任意の線分Ｃをとる。
  　命題１０ー６の系３（作図.長さ・平方で通約可の線分)
  により
  　Ｃと通約できる線分Ａ、Ｂを別々にとる。
  
• 　Ａ∩Ｃ、Ｂ∩Ｃ
  となっている。

　ＡとＢも通約できる
と主張する。

　ＡはＣと通約できる

• 命題の設定による。
• 　Ａ∩Ｃ
  となっている。

から、
　ＡはＣに対し、
　数が数に対する比をもつ。

• 　前節、
  　命題１０ー５（通約可能なら数：数の比）
  による。
• 　Ａ：Ｃ＝数：数
  となっている。

　ＤがＥに対する比をもつ
とせよ。
　　　　　　[......(ａ)]

• 　前節による。
• 　Ａ：Ｃ＝Ｄ：Ｅ（数）
  となっている。

また
　ＣはＢと通約できる

• 　命題の設定による。
• 　Ｃ∩Ｂ
  となっている。

から、
　ＣはＢに対し、
　数が数に対する比をもつ。

• 　前節、
  　命題１０ー５（通約可能なら数：数の比）
  による。
• 　Ｃ：Ｂ＝数：数
  となっている。

　ＦがＧに対する比をもつ
とせよ。
　　　　　　[......(ｂ)]

• 　前節による。
• 　Ｃ：Ｂ＝Ｆ：Ｇ（数）
  となっている。

そして
　任意個の比、
すなわち
　ＤがＥに対する比、
　ＦがＧに対する比
が与えられ、
　順次に
　これらの与えられた比をなす
　数Ｈ、Ｋ、Ｌがとられた
とせよ。

• 　命題７ー３３（構成.任意個の比例で最小数） により
  　Ｄ：Ｅ＝Ｍ：Ｎ（最小）、
  　Ｆ：Ｇ＝Ｏ：Ｐ（最小）
  　をとり、
  　命題８ー４（構成.複数の比で順次に比例する最小の数）
  により、
  　Ｄ：Ｅ＝Ｈ：Ｋ（数）、
  　Ｆ：Ｇ＝Ｋ：Ｌ（数）
  となるように、
  　Ｈ、Ｋ、Ｌ
  　をとる。

そうすれば
　ＤがＥに対するように、
　ＨがＫに対し、
　ＦがＧに対するように、
　ＫがＬに対する。
　　　　　　[......(ｃ)]

• 　前節による。
• 　Ｄ：Ｅ＝Ｈ：Ｋ（数）、
  　Ｆ：Ｇ＝Ｋ：Ｌ（数）
  となっている。

そこで
　ＡがＣに対するように、
　ＤがＥに対し、

• 　（ａ）による。
• 　Ａ：Ｃ＝Ｄ：Ｅ（数）
  となっている。

　他方
　ＤがＥに対するように、
　ＨがＫに対する

• 　（ｃ）による。　
• 　Ｄ：Ｅ＝Ｈ：Ｋ（数）
  となっている。

から、
　ＡがＣに対するように、
　ＨがＫに対する。
　　　　　　[......(１)]

• 　前節、前々節、
  　命題５ー１１（同一の比に同じ比）
  による。
• 　Ａ：Ｃ＝Ｈ：Ｋ（数）
  となっている。

また
　ＣがＢに対するように、
　ＦがＧに対し、

• 　（ｂ）による。
• 　Ｃ：Ｂ＝Ｆ：Ｇ（数）
  となっている。

　他方ＦがＧに対するように、
　ＫがＬに対する

• 　（ｃ）による。
• 　Ｆ：Ｇ＝Ｋ：Ｌ（数）
  になっている。

から、
　ＣがＢに対するように、
　ＫがＬに対する。

• 　前節、前々節、
  　命題５ー１１（同一の比に同じ比）
  による。
• 　Ｃ：Ｂ＝Ｋ：Ｌ（数）
  となっている。

そして
　ＡがＣに対するように、
　ＨがＫに対する。

• 　（１）による。
• 　Ａ：Ｃ＝Ｈ：Ｋ（数）
  になっている。

したがって
　等間隔比により
　ＡがＢに対するように、
　ＨがＬに対する。

• 　前節、前々節、
  　命題７ー１４（数の等間隔比）
  による。
• 　Ａ：Ｂ＝Ｈ：Ｌ（数）
  となっている。

ゆえに
　ＡはＢに対し、
　数Ｈが数Ｌに対する比をもつ。

• 　前節による。
• 　Ａ：Ｂ＝数：数
  となっている。

したがって
　ＡはＢと通約できる。

• 　前節、
  　命題１０ー６（量が数：数なら通約可）
  による。
• 　Ａ∩Ｂ
  となっている。

よって
　同一の量と通約できる量は
　相互にも通約できる。

これが証明すべきことであった。

• 命題１０ー１２は、
  　Ａ∩Ｃ、Ｂ∩Ｃ
  ならば、
  　Ａ∩Ｂ。
  のことである。
  
• 命題１０ー１２は推論用命題である。

  前提	作図・構成	推論
  定義
  公準	1-1補2
  公理
  命題	7-33,8-4,10-6系3	5-11,7-14,10-5,10-6
  その他	コ6(題5-1)

前 　　 次 　　 目次 　　頁頭