ユークリッド原論をどう読むか（１４）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第１０巻
　
命題１０ー１０（作図.平方のみ通約の線分・平方でも非通約の線分）
(作図.２線分;上の正方形が２線分の比)
　定められた線分に対し
　２つの、
　一方は長さにおいてのみ、
　他方は平方においても
　通約できない線分
を見いだすこと。

• 線分は、
  定義の補足（命題１ー１）による。
• 長さにおいて通約は、
  定義１０ー２の補足による。
• 平方において通約は、
  定義１０ー２による。

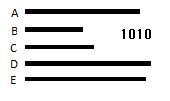
　定められた線分をＡ
とせよ。

• 　「量（について）・・・とせよ」は、
  　コメント６（命題５ー１）
  　参照のこと。
  

このとき
　Ａと
一方は
　長さにおいてのみ、
他方は
　平方においても
　通約できない２線分
を見いださねばならぬ。

　互いに
　平方数が平方数に対する比をもたない、
すなわち
　相似な平面数でない２数Ｂ、Ｃ
が定められ、
　　　　　　[......(ａ)]

• 　「数（について）・・・とせよ」は、
  　コメント４（命題７ー１）
  　参照のこと
• 　命題１０ー１０助の系（非相似平面数は平方数：平方数とならず）
  により、
  　例えば、
  　２×３＝６と３×３＝９
  と定める。
• 　Ｂ：Ｃ≠平方数：平方数
  となっている。
  

　ＢがＣに対するように、
　Ａ上の正方形がＤ上の正方形に対する
ようにされているとせよ。
　　　　　　　[......(ｂ)]

• 　命題１０ー６の系２（作図.平方で数：数となる線分）
  による。
  
• 　Ｂ：Ｃ(数）＝sq(_Ａ)：sq(_Ｄ)
  となっている。

　この仕方はすでに学んだ。

• 　この表現は、
  　原論において初出である。
  

そうすれば
　Ａ上の正方形は
　Ｄ上の正方形と通約できる。
　　　　　　[......(１)]

• 　前々節、
  　命題１０ー６（量が数：数なら通約可）
  による。
• 　sq(_Ａ)∩sq(_Ｄ)
  となっとぃる。

そして
　ＢはＣに対し、
　平方数が平方数に対する比をもたない

• 　（ａ）による。
• 　Ｂ：Ｃ≠平方数：平方数
  となっている。
  

から、
　Ａ上の正方形は
　Ｄ上の正方形に対し、
　平方数が平方数に対する比をもたない。

• 　前節、 （ｂ）、
  　公理の補足３（定義５ー５）(約量(倍量)での代入の原理）
  による。
  
• 　sq(_Ａ)：sq(_Ｄ)≠平方数：平方数
  となっている。

ゆえに
　ＡはＤと長さにおいて通約できない。
　　　　　　[......(２)]

• 　前節、
  　命題１０ー９（長さで通約と平方で通約）
  による。
• 　Ａ¬∩Ｄ
  となっている。

　Ａ、Ｄの比例中項Ｅ
がとられたとせよ。
そうすれば
　ＡがＤに対するように、
　Ａ上の正方形がＥ上の正方形に対する。

• 　前節、
  　命題６ー１３（作図.２線分の比例中項）
  による。
• 　今節から明らかなように、
  　命題６ー１３（作図.２線分の比例中項）
  により、
  
  　上の正方形の比が
  　　与えられた線分の比となる
  　　２線分を、
  作図できる。
  (以下、命題１０ー１０の補足 (作図.２線分;上の正方形が２線分の比)という。)
  
• 　Ａ：Ｅ＝Ｅ：Ｄ、
  　Ａ：Ｄ＝sq(_Ａ)：sq(_Ｅ)
  となっている。

そして
　ＡはＤと長さにおいて通約できない。

• 　（２）による。
• 　Ａ¬∩Ｄ
  となっている。
  

したがって
　Ａ上の正方形は
　Ｅ上の正方形と通約できない。

• 　前節、前々節、
  　公理の補足３（定義５ー５）(約量(倍量)での代入の原理）
  による。
• 　sq(_Ａ)¬∩sq(_Ｅ)
  となっている。
  

ゆえに
　ＡはＥと平方において通約できない。
　　　　　　[......(３)]

• 　前節、
  　定義１０ー２（平方において通約）
  による。
• 　Ａ¬∩^2Ｅ
  となっている。
  

よって
　定められた線分Ａと通約できない
　２線分Ｄ、Ｅが見いだされた。
　Ｄは長さにおいてのみ、

• 　（１）、 （２）による。
• 　Ａ∩^^2Ｄ
  となっている。
  

　Ｅは平方において、

• 　（３）による。
• 　Ａ¬∩^2Ｅ
  となっている。
  

そして
もちろん
　長さにおいても通約できない。

• 　命題１０ー９（長さで通約と平方で通約） による。
• 　Ａ¬∩Ｅ
  となっている。

• 　本命題により、
  　通約できない線分を
  　実際に作図できるようになった。
  また、
  　平方においてのみ通約できる線分
  という概念の根拠が確立した。
  　コメント（命題１０ー７）、
  　命題１０ー６の系３（作図.長さ・平方で通約可の線分)
  　を参照のこと。
  
• 命題１０ー１０は、
  　線分Ａ
  に対して、
  　数Ｂ、Ｃ；Ｂ：Ｃ≠平方数：平方数、
  　線分Ｄ；sq(_Ａ)：sq(_Ｄ)＝Ｂ：Ｃ、
  　線分Ｅ；Ａ、Ｄの比例中項
  をとると、
  　Ａ∩^^2Ｄ、
  　Ａ¬∩^2Ｅ
  のことである。
  
  
• 命題１０ー１０の補足 (作図.２線分;上の正方形が２線分の比)

  前提	作図	推論
  定義
  公準
  公理
  命題	6-13
  その他

• 命題１０ー１０は作図用命題である。

  前提	作図・作図	推論
  定義		10-2
  公準
  公理		補3(義5-5)
  命題	10-6系2	6-13,10-6,10-9,10-10助系
  その他	コ6(題5-1), コ4(題7-1)

前 　　 次 　　 目次 　　頁頭