ユークリッド原論をどう読むか（１２）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第８巻
　
命題８ー１１（平方数の比、比例中項、辺の比の２乗）
（同じ比の２(3)乗の比は同じ）
（平方数の比例中項）

　二つの平方数の間には
　一つの比例中項数があり、
そして
　平方数は平方数に対し、
　辺が辺に対する比の
　２乗の比をもつ。

• 　平方数は、
  定義７ー１９による。
• 　比例中項は、
  定義の補足３（命題６ー８）による。
• 　数は、
  定義７ー２による。
• 　対するは、
  定義の補足３（命題５ー１１）による。
• 　辺は、
  定義７ー１７の補足による。
• 　比は、
  定義５ー３による。
• 　２乗の比は、
  定義５ー９による。

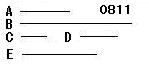
　Ａ、Ｂを平方数とし、
　ＣをＡの辺、
　ＤをＢの辺
とせよ。

• 　「数（について）・・・とせよ」は、
  　コメント４（命題７ー１） 　参照のこと。
• 　Ｃ×Ｃ＝Ａ、Ｄ×Ｄ＝Ｂとなっている。

　Ａ、Ｂの間には
　一つの比例中項数があり、
そして
　ＡはＢに対し
　ＣがＤに対する比の
　２乗の比をもつ
と主張する。

　ＣがＤにかけて
　Ｅをつくる
とせよ。
　　　　　　[......(ａ)]

• 　Ｃ×Ｄ＝Ｅとなっている。

そうすれば
　Ａは平方数であり、
　Ｃはその辺である

• 　命題の設定による。

から、
　Ｃは２乗してＡをつくった。

• 　定義７ー１９による。

同じ理由で
　Ｄも２乗してＢをつくった。

そこで
　ＣはＣ、Ｄにかけて
　それぞれ
　Ａ、Ｅをつくった

• 　前々節、 （ａ）による。

から、
　ＣがＤに対するように、
　ＡがＥに対する。
　　　　　　[......(１)]

• 　前節、
  命題７ー１７（同数を各項にかけても比は同じ）
  による。

同じ理由で
　ＣがＤに対するように、
　ＥがＢに対する。

• 　（ａ）、 命題の設定、
  により、
  　Ｃ×Ｄ＝Ｅ、Ｄ×Ｄ＝Ｂとなり、
  　命題７ー１８（各項を同数にかけても比は同じ）
  による。

ゆえに
　ＡがＥに対するように、
　ＥがＢに対する。

• 　前節、前々節、
  　命題５ー１１（同一の比に同じ比）
  による。

したがって
　Ａ、Ｂの間には
　１つの比例中項数がある。

• 　前節、
  　定義の補足３（命題６ー８）（比例中項）
  による。
• 　Ａ：Ｅ＝Ｅ：Ｂとなっている。

次に
　ＡはＢに対し、
　ＣがＤに対する比の
　２乗の比をもつ
と主張する。

　Ａ、Ｅ、Ｂは
　比例する三つの数である

• 　前々節による。

から、
　ＡはＢに対し、
　ＡがＥに対する比の
　２乗の比をもつ。

• 　前節、
  　定義５ー９（２乗の比）
  による。

ところが
　ＡがＥに対するように、
　ＣがＤに対する。

• 　（１）による。

よって
　ＡはＢに対し、
　辺ＣがＤに対する比の
　２乗の比をもつ。

• 　Ａ：Ｅ＝Ｃ：Ｄ
  のとき
  　命題７ー１７ （同数を各項にかけても比は同じ）
  　命題７ー１８ （各項を同数にかけても比は同じ）
  により
  　Ｃ×Ｃ：Ｃ×Ｄ＝Ｃ×Ｄ：Ｄ×Ｄ
  　＝Ｃ：Ｄ＝Ｅ：Ｆとなり、
  　定義５ー９（２乗の比）
  により、
  　Ａ：Ｂ＝Ｃ×Ｃ：Ｄ×Ｄは
  　Ｃ：Ｄの２乗の比であり、
  また
  　Ｅ：Ｆの２乗の比である。
  さらに、
  　定義５ー１０（３乗の比）
  により、
  　３乗の比も同様である。
  よって、
  　同じ比の２乗の比は同じであり、　
  　同じ比の３乗の比は同じである。　
  
  (以下、命題８ー１１の補足 （同じ比の２(3)乗の比は同じ） という。)
  

　これが証明すべきことであった。

• 　Ａ＝Ｃ^2、Ｂ＝Ｄ^2
  とすると、
  　Ａ：Ｃ×Ｄ＝Ｃ×Ｄ：Ｂであり、
  　Ａ：Ｂ＝（Ｃ：Ｄ）^2
  のことである。
  
• 　本命題の証明
  により、
  　次のことがわかる。
  
  　２つの平方数の比例中項は、
  　各辺の積である。
  (以下、命題８ー１１の補足２ （平方数の比例中項）という。)
  
• 命題８ー１１の補足 （同じ比の２(3)乗の比は同じ）

  前提	作図	推論
  定義		5-9,5-10
  公準
  公理
  命題		7-17,7-18
  その他

• 命題８ー１１の補足２ （平方数の比例中項）

  前提	作図	推論
  定義
  公準
  公理
  命題		8-11
  その他

• 命題８ー１１は推論用命題である。

  前提	作図	推論
  定義		5-9,補3(題6-8),7-19
  公準
  公理
  命題		5-11,7-17,7-18
  その他	コ4(題7-1)

前 　　 次 　　 目次 　　頁頭