ユークリッド原論をどう読むか（１１）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第７巻
　
命題７ー１７（同数を各項にかけても比は同じ）
もし
　ある数が
　２つの数にかけて
　それぞれある数をつくる
ならば、
　これらの２つの積は
　かけられた２数と同じ比をもつ
であろう。

• 数は、 定義７ー２による。
• かけるは、 定義７ー１６による。
• 積は、 定義７ー１６の補足２による。
• 同じ比は、 定義５ー５による。

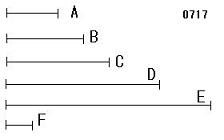
　数Ａは
　２数Ｂ、Ｃにかけて
　Ｄ、Ｅをつくる
とせよ。

• 「数（について）・・・とせよ」は、
  コメント４（命題７ー１） 参照のこと。
  図は、Ａ＝２、Ｂ＝３、Ｃ＝４、Ｄ＝６、Ｅ＝８、Ｆ＝１による。
• 　数Ａ、Ｂ、Ｃ
  に対して、
  　数Ｄ(Ａ×Ｂ)、
  　数Ｅ(Ａ×Ｃ)
  をとっている。

　ＢがＣに対するように、
　ＤがＥに対する
と主張する。

　ＡはＢにかけてＤをつくった
から、
　ＢがＤを割った商は
　Ａのなかにある単位の個数である。

• 定義７ー１６（かける）、
  定義７ー８の補足（商）
  による。
• 　Ｃ＝Ａ×Ｂ
  となっている。

ところが
　単位Ｆが数Ａを割った商も
　Ａのなかにある単位の個数である。

• 定義７ー２（数）
  による。
• 　商(Ａ,単位Ｆ)＝個数(Ａ,単位)＝ａ
  となっている。

それゆえ
　単位Ｆが数Ａを、
　ＢがＤを
　割った商は等しい。

• 公理１ー１（同じものに等しい）
  による。
• 　商(Ａ,単位Ｆ)＝商(Ｄ,Ｂ)＝ａ
  となっている。

ゆえに
　単位Ｆが数Ａに対するように、
　ＢがＤに対する。

• 前節の結果、
  定義７ー２１（比例）
  による。
• 　Ｆ：Ａ＝Ｂ：Ｄ
  となっている。

　同じ理由で
また
　単位Ｆが数Ａに対するように、
　ＣがＥに対する。

• 　Ｆ：Ａ＝Ｃ：Ｅ
  となっている。

したがって
　ＢがＤに対するように、
　ＣがＥに対する。

• 前節、前々節の結果、
  公理１ー１（同じものに等しい）
  による。
• 　Ｂ：Ｄ＝Ｃ：Ｅ
  となっている。

よって
　いれかえて
　ＢがＣに対するように、
ＤがＥに対する。

• 命題７ー１３（比例４数はいれかえても比例）
  による。
• 　Ｂ：Ｃ＝Ｄ：Ｅ
  となっている。

　これが証明すべきことであった。

• 命題７ー１７は推論用命題は
  　Ａ＊Ｂ：Ａ＊Ｃ＝Ｂ：Ｃ
  のことである。
• 命題７ー１７は推論用命題である。

  前提	作図	推論
  定義		7-2,7-8補,7-16,7-21
  公準
  公理		1-1
  命題		7-13
  その他	コ4(題7-1)

前 　　 次 　　 目次 　　頁頭