ユークリッド原論をどう読むか（１２）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第８巻
　
命題８ー１２（立方数の比、比例中項）
（立方数の比例中項）
　２つの立方数の間には
　２つの比例中項数があり、
そして
　立方数は立方数に対し
　辺が辺に対する比の
　３乗の比をもつ。

• 立方数は、
  定義７ー２０による。
• 比例中項は、
  定義の補足３（命題６ー８）による。
• 数は、
  定義７ー２による。
• 対するは、
  定義の補足３（命題５ー１１）による。
• 辺は、
  定義７ー１８の補足による。
• 比は、
  定義５ー３による。
• ３乗の比は、
  定義５ー１０による。

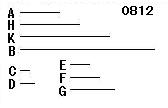
　Ａ、Ｂを立方数
とし、
　ＣをＡの辺、ＤをＢの辺
とせよ。

• 「数（について）・・・とせよ」は、
  　コメント４（命題７ー１）
  　参照のこと。
• Ｃ×Ｃ×Ｃ＝Ａ、
  Ｄ×Ｄ×Ｄ＝Ｂとなっている。

　Ａ、Ｂの間には
　２つの比例中項数があり、
そして
　ＡはＢに対し、
　ＣがＤに対する比の
　３乗の比をもつ
と主張する。
　Ｃが２乗してＥをつくり、
　ＤをかけてＦをつくり、
　Ｄが２乗してＧをつくり、
　Ｃ、ＤがＦにかけて
　それぞれＨ、Ｋをつくる
とせよ。
　　　　　　[......(ａ)]

• 　Ｃ×Ｃ＝Ｅ、Ｃ×Ｄ＝Ｆ、
  　Ｄ×Ｄ＝Ｇ、
  　Ｃ×Ｆ＝Ｈ、Ｄ×Ｆ＝Ｋ
  　となっている。

そうすれば
　Ａは立方数であり、
　Ｃはその辺であり、
　Ｃは２乗してＥをつくった
から、
　Ｃは２乗してＥをつくり、
　ＥにかけてＡをつくった。
　　　　　　[......(１)]

• 　定義７−２０（立方数） により、 　Ｃ×Ｃ＝Ｅ、
  　Ｃ×Ｅ＝Ｃ×Ｃ×Ｃ＝Ａ
  　となっている。

同じ理由で
　Ｄも２乗してＧをつくり、
　ＧにかけてＢをつくった。
　　　　　　[......(２)]

• 　定義７−２０（立方数）
  により、
  　Ｄ×Ｄ＝Ｇ、
  　Ｄ×Ｇ＝Ｄ×Ｄ×Ｄ＝Ｂ
  　となっている。

そして
　ＣはＣ、Ｄにかけて
　それぞれＥ、Ｆをつくった

• 　（ａ）による。

から、
　ＣがＤに対するように、
　ＥがＦに対する。
　　　　　　[......(３)]

• 　命題７ー１７
  　（同数を各項にかけても比は同じ）
  により、
  　Ｃ：Ｄ＝Ｅ：Ｆとなっている。
  

同じ理由で
　ＣがＤに対するように、
　ＦがＧに対する。
　　　　　　[......(４)]

• 　（ａ）
  により、
  　Ｃ×Ｄ＝Ｆ、Ｄ×Ｄ＝Ｇ
  　となり、
  　命題７ー１８
  　（各項を同数にかけても比は同じ）
  により、
  　Ｃ：Ｄ＝Ｆ：Ｇとなっている。
  

また
　ＣがＥ、Ｆにかけて
　それぞれＡ、Ｈをつくった

• 　（１） （ａ）による。

から、
　ＥがＦに対するように、
　ＡがＨに対する。

• 　命題７ー１７
  　（同数を各項にかけても比は同じ）
  により、
  　Ｅ：Ｆ＝Ａ：Ｈとなっている。
  

ところが
　ＥがＦに対するように、
　ＣがＤに対する。

• 　（３）による。

それゆえ
　ＣがＤに対するように、
　ＡがＨに対する。
　　　　　　[......(５)]

• 　前節、前々節、
  　命題５ー１１
  　（同一の比に同じ比）
  により、
  　Ｃ：Ｄ＝Ａ：Ｈとなっている。
  

また
　Ｃ、ＤはＦにかけて
　それぞれＨ、Ｋをつくった

• 　（ａ）による。

から、
　ＣがＤに対するように、
　ＨがＫに対する。
　　　　　　[......(６)]

• 　命題７ー１８
  　（各項を同数にかけても比は同じ）
  により、
  　Ｃ：Ｄ＝Ｈ：Ｋとなっている。
  

また
　ＤがＦ、Ｇにかけて
　それぞれＫ、Ｂをつくった

• 　（ａ）、 （２） による。

から、
　ＦがＧに対するように、
　ＫがＢに対する。

• 　命題７ー１７
  　（同数を各項にかけても比は同じ）
  により、
  　Ｆ：Ｇ＝Ｋ：Ｂとなっている。
  

ところが
　ＦがＧに対するように、
　ＣがＤに対する。

• 　（４）による。

ゆえに
　ＣがＤに対するように、
　ＡがＨに、
　ＨがＫに、
　ＫがＢに対する。

• 　（５）、 （６）、
  　前節、前々節、
  　命題５ー１１
  　（同一の比に同じ比）
  による。

したがって
　Ｈ、ＫはＡ、Ｂの２つの比例中項である。
　　　　　　[......(７)]

• 　定義の補足３（命題６ー８）
  　(比例中項)
  による。

次に、
　ＡはＢに対し、
　ＣがＤに対する比の
　３乗の比をもつと主張する。

　Ａ、Ｈ、Ｋ、Ｂは
　４つの比例する数である

• 　（７）による。

から、
　ＡはＢに対し、
　ＡがＨに対する比の
　３乗の比をもつ。

• 　定義５ー１０（３乗の比） による。

ところが
　ＡがＨに対するように、
　ＣがＤに対する。

• （５）による。

したがって
　ＡはＢに対し、
　ＣがＤに対する比の
　３乗の比をもつ。

• 　命題８ー１１の補足
  　（同じ比の２(3)乗の比は同じ）
  による。

　これが証明すべきことであった。

• 　Ａ＝Ｃ^3、Ｂ＝Ｄ^3
  のとき、
  　Ａ：Ｃ×Ｃ×Ｄ＝
  　Ｃ×Ｃ×Ｄ：Ｃ×Ｄ×Ｄ＝
  　Ｃ×Ｄ×Ｄ：Ｂであり、
  　かつ
  　Ａ：Ｂ＝（Ｃ：Ｄ）^3である。
  
• 　本命題の証明
  により、
  　次のことがわかる。
  
  　２つの立方数の２つの比例中項は、
  　前者の辺の２乗と後者の辺との積と、
  　前者の辺と後者の辺の２乗との積と、
  　である。
  (以下、命題８ー１２の補足 （立方数の比例中項）という。)
  
• 命題８ー１２の補足 （立方数の比例中項）

  前提	作図	推論
  定義
  公準
  公理
  命題		8-12
  その他

• 命題８ー１２は推論用命題である。

  前提	作図	推論
  定義		5-10,補3(題6-8),7-20
  公準
  公理
  命題		5-11,7-18,8-11補
  その他	コ4(題7-1)

前 　　 次 　　 目次 　　頁頭