ユークリッド原論をどう読むか（１２）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第８巻
　
命題８ー１０（単位と２数との間の順次比例挿入項）
もし
　二つの数の双方と
　単位との間に
　順次に比例する数が入る
ならば、
　いくつの数が順次に比例して
　それらの双方と
　単位との間に入ろう
と、
　同じ個数の数が
　順次に比例して
　もとの２数の間にも入る
であろう。

• 　数は、
  定義７ー２による。
• 　単位は、
  定義７ー１による。
• 　順次に比例は、
  定義の補足（命題８ー１）による。

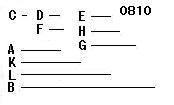
　２数Ａ、Ｂと単位Ｃとの間に
　順次に比例する数
　Ｄ、ＥとＦ、Ｇとが入る
とせよ。

• 「数（について）・・・とせよ」は、
  　コメント４（命題７ー１）
  　参照のこと。
  
• 　準一般的な証明である。
  　コメント２（命題５ー１）参照のこと。
  
• 　双方の数と単位との間に
  　順次に比例する数として
  　入る数の個数は一致せ
  ねばならない。
  
• 　Ｄ、Ｅ、Ｆ、Ｇは、
  　命題８ー８の補足（構成.順次比例項の挿入） による。

　いくつの数が順次に比例して
　Ａ、Ｂの双方と
　単位Ｃとの間に入ろう
と、
　同じ個数の数が順次に比例して
　Ａ、Ｂの間にも入る
であろうと主張する。

　ＤがＦにかけてＨをつくり、
　Ｄ、Ｆの双方がＨにかけて
　Ｋ、Ｌの双方をつくる
とせよ。
　　　　　　[......(ａ)]

そうすれば
　単位Ｃが数Ｄに対するように、
　ＤがＥに対する

• 　命題の設定による。

から、
　単位Ｃが数Ｄを、
　ＤがＥを割った商は等しい。

• 　前節、
  　定義７−２１（比例） による。

ところが
　単位Ｃが数Ｄを割った商は
　Ｄのなかにある単位の数である。

• 　定義７ー８の補足（商） による。

それゆえ
　数ＤがＥを割った商も
　Ｄのなかにある単位の数である。

• 　前節、前々節による。

ゆえに
　Ｄは２乗してＥをつくった。
　　　　　　[......(１)]

• 　前節、
  　命題の補足４（定義７ー１６）
  　（商を割る数にかけると割られる数）
  による。

また
　単位Ｃが数Ｄに対するように、
　ＥはＡに対する

• 　命題の設定による。

から、
　単位Ｃが数Ｄを、
　ＥがＡを割った商は等しい。

• 　前節、
  　定義７−２１（比例）
  による。

ところが
　単位Ｃが数Ｄを割った商は
　Ｄのなかにある単位の個数である。

• 　定義７ー８の補足（商）
  による。

したがって
　ＥがＡを割った商も
　Ｄのなかにある単位の個数である。

• 　前節、前々節による。

それゆえ
　ＤはＥにかけてＡをつくった。

• 　前節、
  　命題の補足４（定義７ー１６）
  　（商を割る数にかけると割られる数）
  による。

同じ理由で
　Ｆは２乗してＧをつくり、
　ＧにかけてＢをつくった。

そして
　Ｄは２乗してＥをつくり、
　ＦにかけてＨをつくった

• 　（１）、 　（ａ）による。
• 　Ｄ×Ｄ＝Ｅ、Ｄ×Ｆ＝Ｈとなっている。

から、
　ＤがＦに対するように、
　ＥがＨに対する。
　　　　　　[......(２)]

• 　命題７ー１７（同数を各項にかけても比は同じ）
  による。

同じ理由で
　ＤがＦに対するように、
　ＨがＧに対する。
　　　　　　[......(３)]

• 　（ａ）、 命題の設定により、
  　Ｄ×Ｆ＝Ｈ、Ｆ×Ｆ＝Ｇとなる
  ので、
  　命題７ー１８（各項を同数にかけても比は同じ）
  による。

ゆえに
　ＥがＨに対するように、
　ＨがＧに対する。

• 　前節、前々節、
  　命題５ー１１（同一の比に同じ比）
  による。

また
　ＤはＥ、Ｈにかけて
　それぞれＡ、Ｋをつくった

• 　命題の設定、 （ａ）による。
• 　Ｄ×Ｅ＝Ａ、Ｄ×Ｈ＝Ｋとなっている。

から、
　ＥがＨに対するように、
　ＡがＫに対する。

• 　前節、
  命題７ー１７（同数を各項にかけても比は同じ）
  による。

ところが
　ＥがＨに対するように、
　ＤがＦに対する。

• 　（２）による。

したがって
　ＤがＦに対するように、
　ＡがＫに対する。
　　　　　　[......(４)]

• 　前節。前々節、
  　命題５ー１１（同一の比に同じ比）
  による。

また
　Ｄ、ＦはＨにかけて
　それぞれＫ、Ｌをつくった

• 　（ａ）による。

から、
　ＤがＦに対するように、
　ＫがＬに対する。
　　　　　　[......(５)]

• 　前節、
  　命題７ー１８（各項を同数にかけても比は同じ）
  による。

ところが
　ＤがＦに対するように、
　ＡがＫに対する。

• 　（４）による。

それゆえ
　ＡがＫに対するように、
　ＫがＬに対する。

• 　前節。前々節、
  　命題５ー１１（同一の比に同じ比）
  による。　

また
　ＦはＨ、Ｇにかけて
　それぞれＬ、Ｂをつくった

• 　（ａ）、 命題の設定による。

から、
　ＨがＧに対するように、
　ＬがＢに対する。

• 　前節、
  命題７ー１７（同数を各項にかけても比は同じ）
  による。

ところが
　ＨがＧに対するように、
　ＤがＦに対する。

• 　（３）による。

ゆえに
　ＤがＦに対するように、
　ＬがＢに対する。

• 　前節。前々節、
  　命題５ー１１（同一の比に同じ比）
  による。　

しかも
　ＤがＦに対するように、
　ＡがＫに、
　ＫがＬに対する
ことが先に証明された。

• 　（４）、 （５）による。

したがって
　ＡがＫに対するように、
　ＫがＬに、
　ＬがＢに対する。

• 　前節。前々節、
  　命題５ー１１（同一の比に同じ比）
  による。　

ゆえに
　Ａ、Ｋ、Ｌ、Ｂは順次に比例する。

• 　前節、
  定義の補足（命題８ー１）（順次に比例）
  による。

よって
　いくつの数が順次に比例して
　Ａ、Ｂの双方と単位Ｃとの間に入ろう
と、
　同じ個数の数が順次に比例して
　Ａ、Ｂの間にも入る
であろう。

　これが証明すべきことであった。

• 　命題８ー９の逆に近い
  が、
  　２数が互いに素であることを
  　前提としない。
  
• 命題８ー１０は推論用命題である。

  前提	作図	推論
  定義		7-8補,7-21,補(題8-1)
  公準
  公理
  命題	8-8補	5-11,補4(義7-16),7-17,7-18
  その他	コ4(題7-1)	コ2(題5-1)

前 　　 次 　　 目次 　　頁頭