ユークリッド原論をどう読むか（８）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第４巻

命題４ー８（正方形の内接円）
与えられた正方形に
　円を内接させること。

• 正方形は、 定義１ー２２ による。
• 円は、 定義１ー１５ による。
• 内接は、 定義４ー５ による。

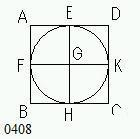
与えられた正方形を
　ＡＢＣＤとせよ。

• 　正方形ＡＢＣＤ
  をとっている。

このとき
　正方形ＡＢＣＤに
　円を内接させねばならぬ。

ＡＤ、ＡＢの双方が
　点Ｅ、Ｆで２等分され、

• 命題１ー１０ （作図・線分の２等分）
  による。
• 　中点Ｅ(ＡＤ)、
  　中点Ｆ(ＡＢ)
  をとっている。

　Ｅを通り
　ＡＢ、ＣＤのどちらかに平行に
　ＥＨがひかれ、 【・・・(a)】

• 命題１ー３１ （作図・平行線）
  による。
• 「どちらか」については、
  　コメント（命題２ー２）を参照のこと
  
• 　交点Ｈ(ＢＣ,平行線(Ｅ,ＡＢ))
  をとっている。

　Ｆを通り
　ＡＤ、ＢＣのどちらかに平行に
　ＦＫがひかれたとせよ。 【・・・(b)】

• 命題１ー３１ （作図・平行線）
  による。
• 「どちらか」については、
  　コメント（命題２ー２）を参照のこと
  
• 　交点Ｋ(ＣＤ,平行線(Ｆ,ＡＤ))
  をとっている。

そうすれば
ＡＫ、ＫＢ、ＡＨ、ＨＤ、ＡＧ、ＧＣ、ＢＧ、ＧＤの
　おのおのは
　平行四辺形であり、 【・・・(1)】

• ＥＨは
  　ＡＢと平行であり、
  ＡＢは
  　ＦＫと交わっているので、
  　 命題１ー３０の補足 (交線に平行な線)
  により
  ＥＨは
  　ＦＫと交わる。
  その交点をＧとする。
• 定義１ー２２の補足２ （平行四辺形）
  による。
• 　交点Ｇ(ＥＨ,ＦＫ)
  をとれば、 　ＡＫ、ＫＢ、ＡＨ、ＨＤ、ＡＧ、ＧＣ、ＢＧ、ＧＤ;平行四辺形
  となっている。

それらの対辺は
　明らかに等しい。

• 命題１ー３４ （平行四辺形の対辺・対角・対角線）
  による。

そして
ＡＤは
　ＡＢに等しく、

• 定義１ー２２ （正方形・矩形・菱形・長斜方形・トラペジオン）
  による。
• 　ＡＤ＝ＡＢ
  となっている。

ＡＥは
　ＡＤの半分であり、
ＡＦは
　ＡＢの半分であるから、

• (a) による。
  
• 　ＡＥ＝ＡＤ／２、
  　ＡＦ＝ＡＢ／２
  となっている。

ＡＥは
　ＡＦに等しい。 【・・・(2)】

• 公理１ー６の補足３ （等しいもののｎ等分、ｎ等分に等しいもの）
  による。
• 　ＡＥ＝ＡＦ
  となっている。

それゆえ
　対辺も等しい。
ゆえに
　ＦＧもＧＥに等しい。

• (1),(2), 公理１ー１の補足 （等しいものに等しい）
  による。
  ＡＥの対辺ＦＧも
  　ＡＦの対辺ＧＥに等しい
  という意味である。
• 　ＦＧ＝ＧＥ
  となっている。

同様にして
ＧＨ、ＧＫの双方は
　ＦＧ、ＧＥの双方に等しい

• (a) によりＦＢはＡＦに、
  　(2) によりＡＦはＡＥに等しく、
  　(1) によりそれぞれの対辺も等しくなり、
  　また同様にして
  　ＥＤ（ＡＥ）はＡＦに等しく、
  　それぞれの対辺も等しくなる
  　という意味である。
• 　(ＧＨ,ＧＫ)＝(ＦＧ,ＧＥ)
  となっている。

　ことも証明しうる。
したがって
　ＧＥ、ＧＦ、ＧＨ、ＧＫの４つは互いに等しい。

• 公理１ー１の補足 （等しいものに等しい）
  による。
• 　ＧＨ＝ＧＫ＝ＦＧ＝ＧＥ
  となっている。

それゆえ
　Ｇを中心とし、
　ＧＥ、ＧＦ、ＧＨ、ＧＫの１つを
　半径として
　円が描かれれば、
　残りの点をも通るであろう。

• 「〜の１つ」については、
  　コメント（命題４ー４）を参照のこと
  
• 　Ｅ、Ｆ、Ｈ、Ｋ;上.円周(Ｇ,ＧＥ)
  となっている。

そして
Ｅ、Ｆ、Ｈ、Ｋにおける角は
　直角であるから、

• 例えば、 Ｅについては、
  　(a) により、
  　ＥＨがＡＢに平行にひかれたから、
  　 命題１ー２９ （平行と錯角、内対角、同側内角）
  により
  　角ＡとＥは等しくなり、
  　Ａが、
  　 定義１ー２２ （正方形・矩形・菱形・長斜方形・トラペジオン）
  により直角であることによる。 他も、同様である。
• 　ＧＥ⊥ＤＡ、
  　ＧＦ⊥ＡＢ、
  　ＧＨ⊥ＢＣ、
  　ＧＫ⊥ＣＤ
  となっている。

　ＡＢ、ＢＣ、ＣＤ、ＤＡに接するであろう。
なぜならもし
　円がＡＢ、ＢＣ、ＣＤ、ＤＡと交わるならば、

• 「なぜならもし」については、
  　コメント（命題１ー４）を参照のこと。
• 背理法の仮定である。

　円の直径に
　その端から直角にひかれた直線が
　円の内部におちることになるであろう。

• 交わるということを
  　言い換えている。

これは
　不合理であることが証明された。

• ＦＫは直径であり、ＡＢはＦＫに直角にひかれた直線となり、
  命題３ー１６ （直径に直角な直線）
  による。

ゆえに
　Ｇを中心とし
　ＧＥ、ＧＦ、ＧＨ、ＧＫの１つを
　半径とする
　円が描かれれば、
　線分ＡＢ、ＢＣ、ＣＤ、ＤＡと
　交わらないであろう。

• 背理法による。

したがって
　それらに接し
　正方形ＡＢＣＤに内接されているであろう。

• 定義４ー５ （内接(円の)）
  による。
• 　ＡＢ;（接）円(Ｇ,ＧＥ)、
  　ＢＣ;（接）円(Ｇ,ＧＥ)、
  　ＣＤ;（接）円(Ｇ,ＧＥ)、
  　ＤＡ;（接）円(Ｇ,ＧＥ)
  となっている。

よって、
　与えられた正方形に円が内接された。

　円(Ｇ,ＧＥ);（内接）正方形ＡＢＣＤ
となっている。 これが作図すべきものであった。

• 命題４ー８は、
  　正方形ＡＢＣＤ
  において、
  　中点Ｅ(ＡＤ)、
  　中点Ｆ(ＡＢ)、
  　交点Ｇ(平行線(Ｅ,ＡＢ),平行線(Ｆ,ＡＤ))
  をとれば、
  　円(Ｇ,ＧＥ);（内接）正方形ＡＢＣＤ
  のことである。
• 命題４ー８は作図用命題である。

  前提	作図	推論
  定義		1-22,1-22補2,4-5
  公準
  公理		1-1補,1-6補3
  命題	1-10,1-30補,1-31	1-29,1-34,3-16
  その他	コ(題2-2) ,コ(題4-4)	背理法, コ(題1-4)fi

前 　　 次 　　 目次 　　頁頭