ユークリッド原論をどう読むか（８）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第４巻

命題４ー９（正方形の外接円）
与えられた正方形に
　円を外接させること。

• 正方形は、 定義１ー２２ による。
• 円は、 定義１ー１５ による。
• 外接は、 定義４ー６ による。

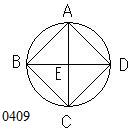
与えられた正方形を
　ＡＢＣＤとせよ。

• 　正方形ＡＢＣＤ
  をとっている。

このとき
　正方形ＡＢＣＤに
　円を外接させねばならぬ。

ＡＣ、ＢＤが結ばれ、

• 公準１ー１ （作図.直線）
  による。
• 　線分ＡＣ、ＢＤ
  をとっている。

　Ｅにおいて互いに交わるとせよ。 【・・・(a)】

• 命題１ー３４の補足３ （平行四辺形の対角線は互いに他を２等分）
  により、
  ＢＤは
  　ＡＣと交わる。
  その交点をＥとする。
• 　交点Ｅ(ＡＣ,ＢＤ)
  をとっている。

そうすれば
ＤＡは
　ＡＢに等しく、

• 命題の設定, 定義１ー２２ （正方形・矩形・菱形・長斜方形・トラペジオン）
  による。
• 　ＤＡ＝ＡＢ
  となっている。

ＡＣは共通であるから、
２辺ＤＡ、ＡＣは
　２辺ＢＡ、ＡＣに等しい。

• 　(ＤＡ、ＡＣ)＝(ＢＡ,ＡＣ)
  となっている。

そして
底辺ＤＣは
　底辺ＢＣに等しい。

• 命題の設定, 定義１ー２２ （正方形・矩形・菱形・長斜方形・トラペジオン）
  による。
• 　ＤＣ＝ＢＣ
  となっている。

それゆえ
角ＤＡＣは
　角ＢＡＣに等しい。

• 命題１ー８ （３辺相等２）
  による。
• 　∠ＤＡＣ＝∠ＢＡＣ
  となっている。

ゆえに
角ＤＡＢは
　ＡＣによって２等分された。
同様にして
　角ＡＢＣ、ＢＣＤ、ＣＤＡのおのおのが
　線分ＡＣ、ＤＢによって２等分された
　ことを証明しうる。 【・・・(1)】

• 　ＡＣ;二等分線(∠ＡＤＢ)、
  　ＡＣ;二等分線(∠ＤＣＢ)、
  　ＤＢ;二等分線(∠ＡＢＣ)、
  　ＤＢ;二等分線(∠ＣＤＡ)
  となっている。

そして
角ＤＡＢは
　ＡＢＣに等しく、

• 命題の設定, 定義１ー２２ （正方形・矩形・菱形・長斜方形・トラペジオン）
  による。
• 　∠ＤＡＢ＝∠ＡＢＣ
  となっている。

角ＥＡＢは
　角ＤＡＢの半分であり、
角ＥＢＡは
　角ＡＢＣの半分であるから、

• (1)による。
• 　∠ＥＡＢ＝∠ＤＡＢ／２、
  　∠ＥＢＡ＝∠ＡＢＣ／２
  となっている。

角ＥＡＢも
　角ＥＢＡに等しい。

• 公理１ー６の補足３ （等しいもののｎ等分、ｎ等分に等しいもの）
  による。
• 　∠ＥＡＢ＝∠ＥＢＡ
  となっている。

したがって
辺ＥＡも
　ＥＢに等しい。 【・・・(2)】

• 命題１ー６ （等しい底角なら二等辺三角形）
  による。
• 　ＥＡ＝ＥＢ
  となっている。

同様にして
ＥＡ、ＥＢの双方が
　《ＥＣ、》ＥＤ［、ＥＣ］の双方に等しい
　ことも証明しうる。
それゆえ
ＥＡ、ＥＢ、ＥＣ、ＥＤの４つは
　互いに等しい。

• 公理１ー１の補足 （等しいものに等しい）
  による。
• 命題１ー３４の補足３ （平行四辺形の対角線は互いに他を２等分）
  によれば、
  　　 ＥＡとＥＣ、ＥＢとＥＤがそれぞれ等しく、
  　(2)により
  　ＥＡとＥＢが等しいことから、
  　 公理１ー１の補足 （等しいものに等しい）
  により
  　４つが等しいと証明できる。 【・・・(3)】
• 　ＥＡ＝ＥＢ＝ＥＣ＝ＥＤ
  となっている。

ゆえに
　 Ｅを中心とし、
　ＥＡ、ＥＢ、ＥＣ、ＥＤの１つを半径として
　円が描かれれば、 【・・・(b)】
　残りの点をも通り、

• 定義１ー１５ （円）
  による。
• 「の１つ」については、
  　 コメント（命題４ー４） を参照のこと
• 　Ａ、Ｂ、Ｃ、Ｄ;上.円周(Ｅ,ＥＡ)
  となっている。

　正方形ＡＢＣＤに外接《され》［し］ているであろう。

• 定義４ー６ （外接(円の)）
  による。
• 　円ＡＢＣＤ(Ｅ,ＥＡ);（外接）正方形
  となっている。

ＡＢＣＤのように
　外接《され》［し］たとせよ。

• (b)では、
  　実際に描いているのではなく、
  　描いたとしたら
  　という立場で表現している。
  そのため、
  　ここで実際に描くことを
  　指示している。
  コメント２（命題４ー４） を参照のこと
  

よって
　与えられた正方形に円が外接《され》［し］た。
これが作図すべきものであった。

• 命題４ー９は、
  　正方形ＡＢＣＤ
  において、
  　線分ＡＣ、ＢＤ、
  　交点Ｅ(ＡＣ,ＢＤ)
  をとれば、
  　円(Ｅ,ＥＡ);（外接）正方形ＡＢＣＤ
  のことである。
  
• 命題４ー９は作図用命題である。

  前提	作図	推論
  定義		1-15,1-22,4-6
  公準	1-1
  公理		1-1補,1-6補3
  命題	1-34補3	1-6,1-8
  その他	コ(題4-4)	コ2(題4-4)

前 　　 次 　　 目次 　　頁頭