ユークリッド原論をどう読むか（８）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第４巻

命題４ー４（作図.三角形の内接円）
「どれか１つ（の１つ）」 「されたとせよ」

与えられた三角形に
　円を内接させること。

• 三角形は、定義１ー１９の補足２ による。
• 円は、定義１ー１５ による。
• 内接は、定義４ー５ による。

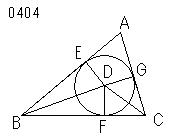
与えられた三角形を
　ＡＢＣとせよ。

• 　△ＡＢＣ
  をとっている。

このとき
　三角形ＡＢＣに
　円を内接させねばならぬ。

角ＡＢＣ、ＡＣＢが
　線分ＢＤ、ＣＤによって
　２等分され、
　点Ｄにおいて相会するとし、 【・・・(a)】

• 命題１ー９ （作図・角の２等分）
  により、
  　角ＡＢＣの２等分線ＢＤをひく。
  ＢＤは
  　命題１ー２１の補足 (三角形の角の分割線は対辺と交わる)
  により
  　辺ＡＣと１点で交わる。
  　その交点をＤ’とする。
  三角形Ｄ’ＣＢにおいて、
  　命題１ー９ （作図・角の２等分）
  により、
  　角Ｄ’ＣＢの２等分線ＣＤ”をひく。
  ＣＤ”は
  　命題１ー２１の補足 (三角形の角の分割線は対辺と交わる)
  により
  　辺ＢＤ’と１点で交わる。
  その点を改めてＤとし、
  　Ｄを溯って用いている。
• 　交点Ｄ(二等分線(∠ＡＢＣ),二等分線(∠ＡＣＢ))
  をとっている。

　Ｄから
　線分ＡＢ、ＢＣ、ＣＡに
　垂線ＤＥ、ＤＦ、ＤＧがひかれたとせよ。 【・・・(b)】

• 命題１ー１２ （作図・線分への垂線）
  による。
• 　垂足Ｅ(Ｄ,ＡＢ)、
  　垂足Ｆ(Ｄ,ＢＣ)、
  　垂足Ｇ(Ｄ,ＣＡ)
  をとっている。

そうすれば
角ＡＢＤは
　角ＣＢＤに等しく、

• (a)による。
• 　∠ＡＢＤ＝∠ＣＢＤ
  となっている。

直角ＢＥＤは
　直角ＢＦＤに等しいから、

• (b)による。
• 　∠ＢＥＤ＝∠ＢＦＤ＝∠Ｒ
  となっている。

ＥＢＤ、ＦＢＤは
　２角が２角に等しく、
　１辺が１辺にひとしい、
　すなわち
　等しい角の１つに対する
　　辺ＢＤを共有する
　２つの三角形である。

• 　(∠ＡＢＤ,∠ＢＥＤ)＝(∠ＣＢＤ,∠ＢＦＤ)、
  　ＢＤ＝ＢＤ
  となっている。

それゆえ
残りの辺も
　残りの辺に等しいであろう。

• 命題１ー２６ （２角挟辺相等）
  による。

ゆえに
ＤＥは
　ＤＦに等しい。

• 　ＤＥ＝ＤＦ
  となっている。

同じ理由で
　ＤＧもＤＦに等しい。

• 　ＤＧ＝ＤＦ
  となっている。

それゆえ
　Ｄを中心とし、
　ＤＥ、ＤＦ、ＤＧの１つを半径として
　円が描かれれば、 【・・・(c)】

• 公準１ー３ （作図.円）
  による。
• 作図の実行に当たっては、
  　「どれか１つ」を
  　半径にして描くということである。
  ＤＥ、ＤＦ、ＤＧは相い等しいので、
  　どれを半径としても
  　結果は同じであるということである。
  　以下、コメント（命題４ー４）(どれか１つ（の１つ）)という。
• コメント（命題２ー２）を参照のこと
  
• 　円(Ｄ,ＤＥ)
  をとっている。

　残りの点をも通り、

• 定義１ー１５ （円）
  による。
• 　Ｅ;上.円周(Ｄ,ＤＥ)、
  　Ｆ;上.円周(Ｄ,ＤＥ)、
  　Ｇ;上.円周(Ｄ,ＤＥ)
  となっている。

　そして
　点Ｅ、Ｆ、Ｇにおける角が
　直角であるから、

• (b)による。
• 　∠ＡＥＤ＝∠ＢＦＤ＝∠ＣＧＤ∠＝Ｒ
  となっている。

　線分ＡＢ、ＢＣ、ＣＡに
　接するであろう。

• 命題３−１６の系 （系．接線は直径と直角）
  による。
• 　ＡＢ（接）円(Ｄ,ＤＥ)、
  　ＢＣ（接）円(Ｄ,ＤＥ)、
  　ＣＡ（接）円(Ｄ,ＤＥ)
  となっている。

なぜなら、
　もし交わるならば、
　円の直径に
　その端から直角にひかれた直線が
　円の内部におちることになるであろう。

• 「なぜならもし」については、
  　コメント（命題１ー４）を参照のこと。
• 定義１ー８の補足（交わる(直線)）
  による。

これは不合理であることが証明された。

• 命題３ー１６（直径に直角な直線）
  による。

ゆえに
　Ｄを中心とし、
　ＤＥ、ＤＦ、ＤＧの１つを
　　半径として描かれた円は
　線分ＡＢ、ＢＣ、ＣＡと
　交わらないであろう。
したがって
　それらに接し、
　三角形ＡＢＣに内接された円であろう。
　それがＦＧＥのように内接されたとせよ。

• (c)では、
  　実際に描いているのではなく、
  　描いたとしたら
  　という立場で表現している。
  そのため、
  　ここで実際に描くことを
  　「されたとせよ」
  　と指示している。
  以下、コメント２（命題４ー４）(されたとせよ)という。
• 初めて登場する表現である。

　 よって
　与えられた三角形ＡＢＣに
　円ＥＦＧが内接された。

• 　円ＥＦＧ;（内接）△ＡＢＣ
  となっている。

これが作図すべきものであった。
　

• 命題４ー４は、
  　△ＡＢＣ
  に対して、
  　交点Ｄ(二等分線(∠ＡＢＣ),二等分線(∠ＡＣＢ))、
  　垂足Ｅ(Ｄ,ＡＢ)
  をとると、
  　円(Ｄ,ＤＥ);（内接）△ＡＢＣ
  のことである。
  
• 命題４ー４は作図用命題である。

  前提	作図	推論
  定義		1-15
  公準	1-3
  公理
  命題	1-9,1-12,1-21補	1-8補,1-26,3-16,3-16系
  その他	コ(題4-4)	背理法,コ2(題4-4),コ2(題1-4)

前 　　 次 　　 目次 　　頁頭